Question

【题目】如图，∠AOB=α°，点P是∠AOB内任意一点，OP=6cm，点M和点N分别是射线OA和射线OB上的动点，若△PMN周长的最小值是6cm，则α的值是（　）

A.15
B.30
C.45
D.60

Answer 1

【答案】B
【解析】解：分别作点P关于OA、OB的对称点C、D，连接CD，
分别交OA、OB于点M、N，连接OC、OD、PM、PN、MN，如图所示：
∵点P关于OA的对称点为D，关于OB的对称点为C，
∴PM=DM，OP=OD，∠DOA=∠POA；
∵点P关于OB的对称点为C，
∴PN=CN，OP=OC，∠COB=∠POB，
∴OC=OP=OD，∠AOB=∠COD，
∵△PMN周长的最小值是6cm，
∴PM+PN+MN=6，
∴DM+CN+MN=6，
即CD=6=OP，
∴OC=OD=CD，
即△OCD是等边三角形，
∴∠COD=60°，
∴∠AOB=30°；
故选：B．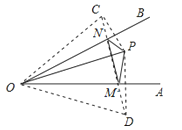

【考点精析】通过灵活运用轴对称-最短路线问题，掌握已知起点结点，求最短路径；与确定起点相反，已知终点结点，求最短路径；已知起点和终点，求两结点之间的最短路径；求图中所有最短路径即可以解答此题．