练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

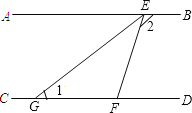
    【题目】如图，AB∥CD，直线 EF 分别交 AB、CD于 点 E、F，EG 平分∠AEF，

    （1）求证：△EGF 是等腰三角形．

    （2）若∠1=40°，求∠2 的度数．

    【答案】（1）证明见详解；（2）100°

    【解析】

    （1）根据平行线的性质求出∠1=∠AEG，求出∠AEG=∠FEG，推出∠1=∠FEG，根据等腰三角形的判定推出即可；
    （2）求出∠AEF的度数，根据邻补角定义求出即可．

    （1）证明：∵AB∥CD，
    ∴∠1=∠AEG，
    ∵EG平分∠AEF，
    ∴∠AEG=∠FEG，
    ∴∠1=∠FEG，
    ∴FE=FG，
    即△EGF是等腰三角形；

    （2）解：∵∠1=40°，∠1=∠AEG=∠FEG，
    ∴∠AEF=40°+40°=80°，
    ∴∠2=180°-80°=100°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

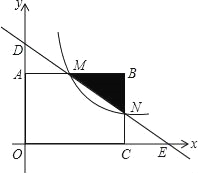
    【题目】如图，在直角坐标系中，矩形OABC的顶点O与坐标原点重合，顶点A，C分别在坐标轴上，顶点B的坐标为（4，2），过点D（0，3）和E（6，0）的直线分别与AB，BC交于点M，N．

    （1）求直线DE的解析式和点M的坐标；

    （2）若反比例函数y=（x＞0）的图象经过点M，在该反比例函数的图象上是否存在一点P，使△PMN的面积等于△OMN的面积的一半，若存在，求点P的坐标，若不存在，请说明理由．

    （3）若反比例函数y=（x＞0）的图象与△MNB有公共点，请直接写出m的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）解不等式

    （2）解不等式组：并将其解集表示在如图所示的数轴上

    （3），并写出不等式组的整数解.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

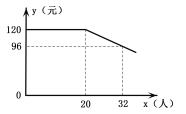
    【题目】随着人们生活水平的提高，短途旅行日趋火爆.我市某旅行社推出“辽阳—葫芦岛海滨观光一日游”项目，团队人均报名费用y（元）与团队报名人数x（人）之间的函数关系如图所示，旅行社规定团队人均报名费用不能低于88元.旅行社收到的团队总报名费用为w（元）.

    （1）直接写出当x≥20时，y与x之间的函数关系式及自变量x的取值范围；

    （2）儿童节当天旅行社收到某个团队的总报名费为3000元，报名旅游的人数是多少？

    （3）当一个团队有多少人报名时，旅行社收到的总报名费最多？最多总报名费是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我们知道，任意一个正整数n都可以进行这样的分解：n=p×q（p，q是正整数，且p≤q），在n的所有这种分解中，如果p，q两因数之差的绝对值最小，我们就称p×q是n的最佳分解，并规定：F（n）=，例如12可以分解成1×12,2×6或3×4，因为12-1＞6-2＞4-3，所有3×4是最佳分解，所以F（12）=.

    （1）如果一个正整数a是另外一个正整数b的平方，我们称正整数a是完全平方数，求证：对任意一个完全平方数m，总有F（m）=1.

    （2）如果一个两位正整数t，t=10x+y（1≤x≤y≤9,x,y为自然数），交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为18，那么我们称这个数t为“吉祥数”，求所有“吉祥数”中F（t）的最大值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

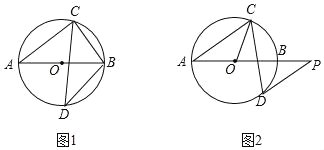
    【题目】已知AB是⊙O的直径，弦CD与AB相交，∠BAC＝40°．

    （1）如图1，若D为弧AB的中点，求∠ABC和∠ABD的度数；

    （2）如图2，过点D作⊙O的切线，与AB的延长线交于点P，若DP∥AC，求∠OCD的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

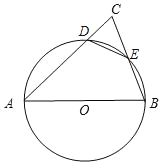
    【题目】如图，AB为⊙O的直径，△ABC的边AC，BC分别与⊙O交于D，E，若E为的中点．

    （1）求证：DE＝EC；

    （2）若DC＝2，BC＝6，求⊙O的半径

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，如果点P的横坐标和纵坐标相等，则称点P为和谐点．例如点（1，1），（-，-），（-，-），…，都是和谐点．
    （1）分别判断函数y=-2x+1和y=x2+1的图象上是否存在和谐点，若存在，求出其和谐点的坐标；
    （2）若二次函数y=ax2+4x+c（a≠0）的图象上有且只有一个和谐点（，），且当0≤x≤m时，函数y=ax2+4x+c-（a≠0）的最小值为-3，最大值为1，求m的取值范围．
    （3）直线l：y=kx+2经过和谐点P，与x轴交于点D，与反比例函数G：y=的图象交于M，N两点（点M在点N的左侧），若点P的横坐标为1，且DM+DN＜3，请直接写出n的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某中学现有在校学生 1250 人，为了解本校学生的课余活动情况，采取随机抽样的方法从阅读、运动、娱乐、其它四个方面调查了若干名学生，并将调查的结果绘制了 如下两幅不完整的统计图，请你根据图中提供的信息解答下列问题：

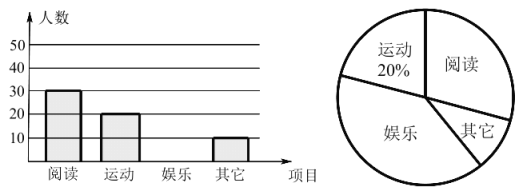
    （1）本次调査共取了多少名学生？

    （2）通过计算补全条形图，并求出扇形统计图中阅读部分圆心角的度数；

    （3）请你估计该中学在课余时间参加阅读和其他活动的学生一共有多少名

    查看答案和解析>>

    同步练习册答案