
【题目】在平面直角坐标系中,如果点P的横坐标和纵坐标相等,则称点P为和谐点.例如点(1,1),(-![]() ,-
,-![]() ),(-
),(-![]() ,-
,-![]() ),…,都是和谐点.
),…,都是和谐点.
(1)分别判断函数y=-2x+1和y=x2+1的图象上是否存在和谐点,若存在,求出其和谐点的坐标;
(2)若二次函数y=ax2+4x+c(a≠0)的图象上有且只有一个和谐点(![]() ,
,![]() ),且当0≤x≤m时,函数y=ax2+4x+c-
),且当0≤x≤m时,函数y=ax2+4x+c-![]() (a≠0)的最小值为-3,最大值为1,求m的取值范围.
(a≠0)的最小值为-3,最大值为1,求m的取值范围.
(3)直线l:y=kx+2经过和谐点P,与x轴交于点D,与反比例函数G:y=![]() 的图象交于M,N两点(点M在点N的左侧),若点P的横坐标为1,且DM+DN<3
的图象交于M,N两点(点M在点N的左侧),若点P的横坐标为1,且DM+DN<3![]() ,请直接写出n的取值范围.
,请直接写出n的取值范围.
【答案】(1)不存在;(2)2≤m≤4;(3)-![]() <n<0或0<n<1.
<n<0或0<n<1.
【解析】
(1)根据和谐点的横坐标与纵坐标相同,可得关于a的方程,根据解方程,可得答案.
(2)根据和谐点的概念令ax2+4x+c=x,即ax2+3x+c=0,由题意,△=32-4ac=0,即4ac=9,方程的根为![]() ,从而求得a=-1,c=
,从而求得a=-1,c=![]() ,所以函数y=ax2+4x+c-
,所以函数y=ax2+4x+c-![]() =-x2+4x-3,根据函数解析式求得顶点坐标与纵坐标的交点坐标,根据y的取值,即可确定x的取值范围.
=-x2+4x-3,根据函数解析式求得顶点坐标与纵坐标的交点坐标,根据y的取值,即可确定x的取值范围.
(3)根据题意得出当n>0时,以及当n<0时,分别利用数形结合得出n的取值.
(1)存在,
令-2x+1=x,解得x=![]() ,
,
∴函数y=-2x+1的图象上有一个和谐点(![]() ,
,![]() );
);
令x2+1=x,即x2-x+1=0,
∵根的判别式△=(-1)2-4×1×1=-3<0,
∴方程x2-x+1=0无实数根,
∴函数y=x2+1的图象上不存在和谐点.
(2)令ax2+4x+c=x,即ax2+3x+c=0,
由题意,△=32-4ac=0,即4ac=9,
又方程的根为![]() ,
,
解得a=-1,c=![]() .
.
故函数y=ax2+4x+c![]() ,即y=-x2+4x-3,
,即y=-x2+4x-3,
如图1,该函数图象顶点为(2,1),与y轴交点为(0,-3),由对称性,该函数图象也经过点(4,-3).

由于函数图象在对称轴x=2左侧y随x的增大而增大,在对称轴右侧y随x的增大而减小,且当0≤x≤m时,函数y=-x2+4x-3的最小值为-3,最大值为1,
∴2≤m≤4.
(3)![]() <n<0,或0<n<1.
<n<0,或0<n<1.
∵y=kx+2经过和谐点P,
∴y=x,
∴x=kx+2,
∴点P的横坐标为1,
∴k=-1,
∴直线l为:y=-x+2,
分两种情况:
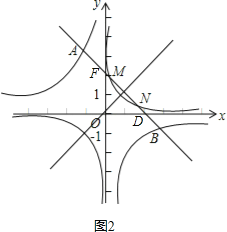
①如图2,当
∵y=-x+2,与x轴交于点D(2,0),与y轴交于点F(0,2),
∴DF=2![]() ,
,
∴DM+DN<3![]() ,
,
∴只要y=-x+2与y=![]() 有交点坐标即可,
有交点坐标即可,
∴-x+2=![]() ,
,
整理得:x2-2x+n=0,
∴b2-4ac>0,
∴4-4n>0,
解得:n<1,
则0<n<1;
②如图3,
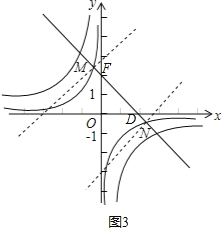
当n<0时,当DM+DN=3![]() ,
,
则DN=FM=![]() ,
,
∵y=-x+2,与x轴交于点D(2,0),与y轴交于点F(0,2),
∴可求出M(-![]() ,
,![]() ),
),
则xy=n=-![]() ,
,
则-![]() <n<0.
<n<0.
综上,当-![]() <n<0或0<n<1时,反比例函数G2的图象与直线l有两个公共点M,N,且DM+DN<3
<n<0或0<n<1时,反比例函数G2的图象与直线l有两个公共点M,N,且DM+DN<3![]() .
.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
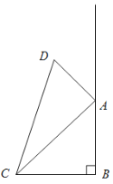
【题目】如图,四边形![]() 为某街心公园的平面图,经测量
为某街心公园的平面图,经测量![]() 米,
米,![]() 米,且
米,且![]() .
.
(1)求![]() 的度数;
的度数;
(2)若![]() 为公园的车辆进出口道路(道路的宽度忽略不计),工作人员想要在点
为公园的车辆进出口道路(道路的宽度忽略不计),工作人员想要在点![]() 处安装一个监控装置来监控道路
处安装一个监控装置来监控道路![]() 的车辆通行情况,已知摄像头能监控的最大范围为周围的100米(包含100米),求被监控到的道路长度为多少?
的车辆通行情况,已知摄像头能监控的最大范围为周围的100米(包含100米),求被监控到的道路长度为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
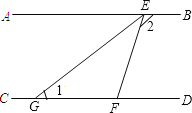
【题目】如图,AB∥CD,直线 EF 分别交 AB、CD于 点 E、F,EG 平分∠AEF,
(1)求证:△EGF 是等腰三角形.
(2)若∠1=40°,求∠2 的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
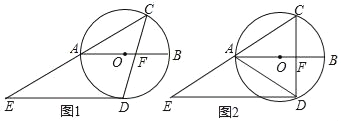
【题目】如图,⊙O的直径AB的长为2,点C在圆周上,∠CAB=30°.点D是圆上一动点,DE∥AB交CA的延长线于点E,连接CD,交AB于点F.
(1)如图1,当DE与⊙O相切时,求∠CFB的度数;
(2)如图2,当点F是CD的中点时,求△CDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知点A的坐标为(3,a)(其中a>4),射线OA与反比例函数y=![]() 的图象交于点P,点B、C分别在函数y=
的图象交于点P,点B、C分别在函数y=![]() 的图象上,且AB∥x轴,AC∥y轴;
的图象上,且AB∥x轴,AC∥y轴;
(1)当点P横坐标为2,求直线AO的表达式;
(2)连接CO,当AC=CO时,求点A坐标;
(3)连接BP、CP,试猜想:![]() 的值是否随a的变化而变化?如果不变,求出
的值是否随a的变化而变化?如果不变,求出![]() 的值;如果变化,请说明理由.
的值;如果变化,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步发展基础教育,自2014年以来,某县加大了教育经费的投入,2014年该县投入教育经费6000万元。2016年投入教育经费8640万元。假设该县这两年投入教育经费的年平均增长率相同。
(1)求这两年该县投入教育经费的年平均增长率;
(2)若该县教育经费的投入还将保持相同的年平均增长率,请你预算2017年该县投入教育经费多少万元。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了调查甲,乙两台包装机分装标准质量为![]() 奶粉的情况,质检员进行了抽样调查,过程如下.请补全表一、表二中的空,并回答提出的问题.
奶粉的情况,质检员进行了抽样调查,过程如下.请补全表一、表二中的空,并回答提出的问题.
收集数据:
从甲、乙包装机分装的奶粉中各自随机抽取10袋,测得实际质量(单位:![]() )如下:
)如下:
甲:394,400,408,406,410,409,400,400,393,395
乙:402,404,396,403,402,405,397,399,402,398
整理数据:
表一
频数种类 质量( | 甲 | 乙 |
| ____________ | 0 |
| 0 | 3 |
| 3 | 1 |
| 0 | ____________ |
| ____________ | 1 |
| 3 | 0 |
分析数据:
表二
种类 | 甲 | 乙 |
平均数 | 401.5 | 400.8 |
中位数 | ____________ | 402 |
众数 | 400 | ____________ |
方差 | 36.85 | 8.56 |
得出结论:
包装机分装情况比较好的是______(填甲或乙),说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
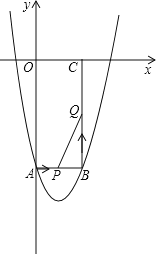
【题目】如图所示,在平面直角坐标系xOy中,矩形OABC的边长OA、OC分别为12cm、6cm,点A、C分别在y轴的负半轴和x轴的正半轴上,抛物线y=ax2+bx+c经过点A、B,且18a+c=0.
(1)求抛物线的解析式.
(2)如果点P由点A开始沿AB边以1cm/s的速度向终点B移动,同时点Q由点B开始沿BC边以2cm/s的速度向终点C移动.
①移动开始后第t秒时,设△PBQ的面积为S,试写出S与t之间的函数关系式,并写出t的取值范围.
②当S取得最大值时,在抛物线上是否存在点R,使得以P、B、Q、R为顶点的四边形是平行四边形?如果存在,求出R点的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在城镇化建设中,开发商要处理A地大量的建筑垃圾,A地只能容纳1台装卸机作业,装卸机平均每6分钟可以给工程车装满一车建筑垃圾,每辆工程车要将建筑垃圾运送至20千米的B处倾倒,每次倾倒时间约为1分钟,倾倒后立即返回A地等候下一次装运,直到装运完毕;工程车的平均速度为40千米/时.
(1)一辆工程车运送一趟建筑垃圾(从装车到返回)需要多少分钟?
(2)至少安排多少辆工程车既能保证装卸机不空闲,又能保证工程车最少等候时间?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com