练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16．如图，已知CD⊥AB，FH⊥AB，∠1与∠2互补，试说明∠AED=∠ACB的理由．

    分析 由条件可证明CD∥FH，进一步可证明DE∥BC，根据平行线的性质可证明∠AED=∠ACB．

    解答 解：∵CD⊥AB，FH⊥AB，
    ∴CD∥FH，
    ∴∠2+∠HCD=180°，
    ∵∠1和∠2互补，即∠1+∠2=180°，
    ∴∠1=∠HCD，
    ∴DE∥BC，
    ∴∠AED=∠ACB．

    点评 本题主要考查平行线的判定和性质，掌握平行线的判定和性质是解题的关键，即①两直线平行?同位角相等，②两直线平行?内错角相等，③两直线平行?同旁内角互补，④a∥b，b∥c⇒a∥c．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

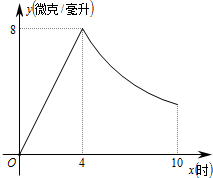    6．某药品研究所开发一种抗菌新药，经多年动物实验，首次用于临床人体实验．测得成人服药后血液中药物浓度y（微克/毫升）与服药时间x小时之间的函数关系如图所示（当4≤x≤10时，y与x成反比）．
     （1）根据图象分别求出血液中药物浓度上升和下降阶段y与x之间的函数关系式；
    （2）若血液中药物浓度不低于4微克/毫升的持续时间不低于5小时，则称药物治疗有效，请问这种抗菌新药可以作为有效药物投入生产吗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．将分式$\frac{xy}{x+y}$中的x，y的值同时扩大10倍，则分式的值（　　）
    A．扩大100倍B．扩大10倍C．不变D．缩小为原来的$\frac{1}{10}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．下列因式分解完全正确的是（　　）
    A．-2a2+4a=-2a（a+2）B．-4x2-y2=-（2x+y）2
    C．a2-8ab+16b2=（a+4b）2D．2x2+xy-y2=（2x-y）（x+y）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．已知$\frac{3x-2xy+3y}{x+xy+y}$=$\frac{1}{2}$，则代数式（x-1）（y-1）的值为1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．解关于x的不等式：$\frac{1-3x}{{a}^{2}}$-12＜$\frac{4-18x}{a}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．如图，图1、图2分别是5×5的网格，网格中每个小正方形的边长均为1，点A、点B、点C的端点在小正方形的顶点上，请在图1、图2中各画一个四边形ABCD，所画四边形ABCD的顶点都在小正方形的顶点上，分别满足以下要求：

    （1）在图1的网格中，画一个对角相等四边形；
    （2）在图2中网格中，画一个对角互补四边形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．（1）计算：（-2）2+3-1-$\root{3}{8}$；
    （2）计算：（x+$\frac{1}{x-2}$）÷（$\frac{1}{x-2}$+1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

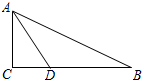    2．已知，如图，在Rt△ABC中，∠C=90°，∠BAC的角平分线AD交BC边于D．
    （1）用尺规在AB边上作点O，并以点O为圆心作⊙O，使它过A、D两点．（不写作法，保留作图痕迹），再判断直线BC与⊙O的位置关系，并说明理由．
    （2）若（1）中的⊙O与AB边的另一个交点为E，AB=6，BD=2$\sqrt{3}$，求线段BD、BE与劣弧DE所围成的图形面积．（结果保留根号和π）

    查看答案和解析>>

    同步练习册答案