
【题目】如图,![]() 为
为![]() 的中线,点
的中线,点![]() 在
在![]() 的延长线上的点,连接
的延长线上的点,连接![]() ,且
,且![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() ,则
,则![]() 的长为________________.
的长为________________.

【答案】3
【解析】
过点A作AF⊥EF于点F,通过证明△AFD≌△BHD(AAS),Rt△CAF≌ Rt△EBH(HL),得到BH= HD+DF=2DH,又因为 ![]() 为
为![]() 的中线,
的中线,![]() ,所以S△BHD=
,所以S△BHD=![]() S△BHA=
S△BHA=![]() ×18=9=
×18=9=![]() ×HD·HB=
×HD·HB=![]() ×HD·2HD,从而求解.
×HD·2HD,从而求解.
解:如图:过点A作AF⊥EF于点F,
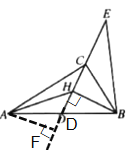
∵![]() 为
为![]() 的中线,
的中线,![]() ,
,
∴AD=BD, ∠AFD=∠BHD=90°,
又∵∠ADF=∠BDH,
∴△AFD≌△BHD(AAS),
∴AF=BH,FD=HD,
∵在Rt△CAF和 Rt△EBH中,![]()
∴Rt△CAF≌ Rt△EBH(HL)
∴EH=CF,
∴EH-CH=CF-CH,即EC=HF
∵BH=EC,EC=HF=HD+DF,HD=DF
∴BH= HD+DF=2DH,
∵![]() 为
为![]() 的中线,
的中线,![]() ,
,
∴S△BHD=![]() S△BHA=
S△BHA=![]() ×18=9=
×18=9=![]() ×HD·HB=
×HD·HB=![]() ×HD·2HD,
×HD·2HD,
解得:HD=3.
故答案为:3.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图1,四边形ABCD是菱形,AD=5,过点D作AB的垂线DH,垂足为H,交对角线AC于M,连接BM,且AH=3.
(1)求证:DM=BM;
(2)求MH的长;
(3)如图2,动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,求S与t之间的函数关系式;
(4)在(3)的条件下,当点P在边AB上运动时是否存在这样的 t值,使∠MPB与∠BCD互为余角,若存在,则求出t值,若不存,在请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )

A. 当AB=BC时,它是菱形 B. 当AC⊥BD时,它是菱形
C. 当∠ABC=90°时,它是矩形 D. 当AC=BD时,它是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
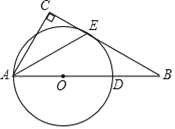
【题目】如图,Rt△ABC,∠C=90°,点D为AB上的一点,以AD为直径的⊙O与BC相切于点E,连接AE.
(1)求证:AE平分∠BAC;
(2)若AC=8,OB=18,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“安全教育平台”是中国教育学会为方便学长和学生参与安全知识活动、接受安全提醒的一种应用软件.某校为了了解家长和学生参与“防溺水教育”的情况,在本校学生中随机抽取部分学生作调查,把收集的数据分为以下4类情形:A.仅学生自己参与;B.家长和学生一起参与;
C.仅家长自己参与; D.家长和学生都未参与.

请根据图中提供的信息,解答下列问题:
(1)在这次抽样调查中,共调查了________名学生;
(2)补全条形统计图,并在扇形统计图中计算C类所对应扇形的圆心角的度数;
(3)根据抽样调查结果,估计该校2000名学生中“家长和学生都未参与”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,O是锐角三角形ABC内一点,∠AOB=∠BOC=∠COA=120°,P是△ABC内不同于O的另一点,△A′BO′、△A′BP′分别由△AOB、△APB旋转而得,旋转角都为60°,则下列结论中正确的有( ).(提示:有一个角是60°的等腰三角形是等边三角形)
①△O′BO为等边三角形,且A′、O′、O、C在一条直线上.
②A′O′+O′O=AO+BO. ③A′P′+P′P=PA+PB.
④PA+PB+PC>AO+BO+CO.
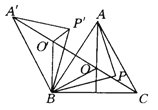
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,边长为a的正方形发生形变后成为边长为a的菱形,如果这个菱形的一组对边之间的距离为h,我们把![]() 的值叫做这个菱形的“形变度”.例如,当形变后的菱形是如图2形状(被对角线BD分成2个等边三角形),则这个菱形的“形变度”为2:
的值叫做这个菱形的“形变度”.例如,当形变后的菱形是如图2形状(被对角线BD分成2个等边三角形),则这个菱形的“形变度”为2:![]() .如图3,正方形由16个边长为1的小正方形组成,形变后成为菱形,△AEF(A、E、F是格点)同时形变为△A′E′F′,若这个菱形的“形变度”k=
.如图3,正方形由16个边长为1的小正方形组成,形变后成为菱形,△AEF(A、E、F是格点)同时形变为△A′E′F′,若这个菱形的“形变度”k=![]() ,则S△A′E′F′=__
,则S△A′E′F′=__

查看答案和解析>>
科目:初中数学 来源: 题型:
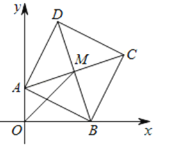
【题目】如图,在平面直角坐标系中,正方形ABCD顶点A的坐标为(0,4),B点在x轴上,对角线AC,BD交于点M,OM=6![]() ,则点C的坐标为_____.
,则点C的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB经过圆心O,交⊙O于A、C两点,点D在⊙O上,∠A=∠B=30°.
(1)求证:BD是⊙O的切线;
(2)若点N在⊙O上,且DN⊥AB,垂足为M,NC=10,求AD的长.
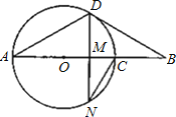
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com