
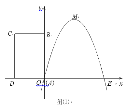
����Ŀ��ijũ�����о���һ�����͵Ļ���ժ���豸��һ���з��ɱ�Ϊÿ̨6��Ԫ����ժ������������![]() (̨)���ۼ�
(̨)���ۼ�![]() (��Ԫ/̨)֮����ں�����ϵ��
(��Ԫ/̨)֮����ں�����ϵ��![]() ��
��
��1��������ժ����һ�����۵�����Ϊ![]() (��Ԫ)����һ������ʱ������ռ�г��ݶ�(��ʾ�����������ܴ�)��ǰ��������ﵽ32��Ԫ����ʱ�ۼ�Ϊ���٣�
(��Ԫ)����һ������ʱ������ռ�г��ݶ�(��ʾ�����������ܴ�)��ǰ��������ﵽ32��Ԫ����ʱ�ۼ�Ϊ���٣�
��2�����ڻ�����Ҫ��û����������ӳ����豸��������Ͷ����7��Ԫ�о����ѣ�ʹ�û�������һ������з��ɱ�ÿ̨������1��Ԫ����������������ս�Ա��ֲ��䣬�����ڶ�������������ﵽ63��Ԫʱ���û�����̨���ۼ�Ϊ���٣�
���𰸡���1������ռ�г��ݶ��ǰ��������Ҫ�ﵽ32��Ԫ����ʱ�ۼ�Ϊ8��Ԫ/̨����2��Ҫʹ��������ﵽ63��Ԫ�����ۼ�Ӧ��Ϊ10��Ԫ/̨��
��������
��1���ȸ��ݵ�����ϵʽ��������=���ۼ�-�ɱ���![]() ���������г�������ϵʽ���ٽ�
���������г�������ϵʽ���ٽ�![]() ���뺯����ϵʽ�ó�������⼴�ã�
���뺯����ϵʽ�ó�������⼴�ã�
��2���ȸ��ݵ�����ϵʽ��������=���ۼ�-�³ɱ���![]() ������-7���г�������ϵʽ���ٽ�
������-7���г�������ϵʽ���ٽ�![]() ���뺯����ϵʽ�ó�������⼴�ã�
���뺯����ϵʽ�ó�������⼴�ã�
��1�����������г�������ϵʽ���£�
![]()
��![]() ʱ��
ʱ��![]() ��
��
���![]() ��
��![]() ��
��
��Ҫ��ռ�г��ݶ�
��![]() ��
��
������ռ�г��ݶ��ǰ��������Ҫ�ﵽ32��Ԫ����ʱ�ۼ�Ϊ8��Ԫ/̨��
��2�����ͳɱ�֮��ÿ̨�ijɱ�Ϊ5��Ԫ��ÿ̨����Ϊ![]() ��Ԫ��������
��Ԫ��������![]() ��
��
���������![]() ��
��
��![]() ʱ��
ʱ��![]() �����
�����![]() ��
��![]() ��
��
��Ҫ��������������������ս��
��![]()
��Ҫʹ��������ﵽ63��Ԫ�����ۼ�Ӧ��Ϊ10��Ԫ/̨��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��1������֪�����߾�������ԭ��O��x������һ��E������M������Ϊ(2��4)������ABCD�Ķ���A���O�غϣ�AD��AB�ֱ���x�ᡢy���ϣ���AD=2��AB=3��
��1����ֱ��y=3�������߽�������ꣻ
��2��������ABCD��ÿ��1����λ���ȵ��ٶȴ�ͼ����ʾ��λ����x�������������ƽ���ƶ���ͬʱһ����PҲ����ͬ���ٶȴӵ�A������B�����ƶ����������˶���ʱ��Ϊt�루0��t��3����ֱ��AB��������ߵĽ���ΪN����ͼ��2����ʾ����
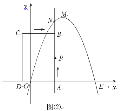
�ٵ�![]() ʱ���жϵ�P�Ƿ���ֱ��ME�ϣ���˵�����ɣ�
ʱ���жϵ�P�Ƿ���ֱ��ME�ϣ���˵�����ɣ�
������P��N��C��DΪ����Ķ�������ΪS������S�Ƿ�������ֵ�������ڣ����������ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣�������y��x2����a+1��x+a��x�ύ��A��B���㣨��Aλ�ڵ�B����ࣩ����y�ύ�ڵ�C����֪��ABC�����Ϊ6��
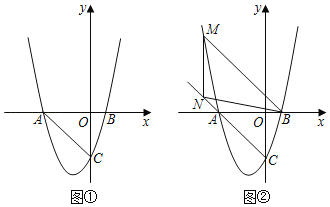
��1����������������Ӧ�ĺ�������ʽ��
��2�������������Ƿ����һ��P��ʹ�á�POB����CBO�������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
��3����ͼ�ڣ�M����������һ�㣬N������CA�ϵ�һ�㣬��M��N������ڵڶ������ڣ�A��N��λ��ֱ��BMͬ��IJ�ͬ���㣮����M��x��ľ���Ϊd����MNB�����Ϊ2d���ҡ�MAN����ANB�����N�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���� AOBC ���������������ֱ�Ϊ O(0��0)��A(0��3)�� B(4��0)�������²�����ͼ�����Ե� O ΪԲ�ģ��ʵ�����Ϊ�뾶������ �ֱ� OC��OB �ڵ� D��E���ڷֱ��Ե� D��E ΪԲ�ģ����� ![]() DE �ij�Ϊ�뾶�����������ڡ�BOC �ڽ��ڵ� F���������� OF������ BC�ڵ� G����� G ������Ϊ( )
DE �ij�Ϊ�뾶�����������ڡ�BOC �ڽ��ڵ� F���������� OF������ BC�ڵ� G����� G ������Ϊ( )
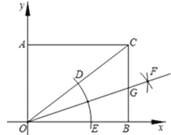
A. (4�� ![]() )B. (
)B. ( ![]() ��4)C. (
��4)C. ( ![]() ��4)D. (4��
��4)D. (4�� ![]() )
)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУΪ���������ݹ�����ϯ�����������������ݽ���ʩ�����죮��ͼ��Ϊ�����ݸ���Ľ���ʾ��ͼ����֪ԭ��λ����ߵ�A�������Ǧֱ�߶�AC����Ϊ15�ף�ԭ����AB����б�ǡ�ABCΪ45����ԭ�½�B�볡��������˶����߽�İ�ȫ����BDΪ5�ף��������ʩ�����ṩ����Ʒ���ʩ��������λ����ߵ�E�������Ǧֱ�߶�EG���ȱ���15�ײ��䣬ʹA��E��������Ϊ2�ף�ʹ���������EF����б�ǡ�EFGΪ37�㣮��ѧУҪ�����½�F���볡��������˶����߽�İ�ȫ����FD���ٱ���2.5�ף���FD��2.5��������ʩ�����ṩ����Ʒ����Ƿ����㰲ȫҪ���أ���˵�����ɣ����ο����ݣ�sin37����![]() ��tan37����
��tan37����![]() ��
��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����y����һ������M��x���ƽ���ߣ���˫����y=![]() �ڵ�A����˫����
�ڵ�A����˫����![]() �ڵ�B����C����D��x�����˶�����ʼ�ձ���DC��AB����ƽ���ı���ABCD������ǣ�������
�ڵ�B����C����D��x�����˶�����ʼ�ձ���DC��AB����ƽ���ı���ABCD������ǣ�������
A. 7 B. 10 C. 14 D. 28
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����������һ�ֽ��������еIJ�Ʒ��������Ϊ20Ԫ![]() ����Ϊ�˵��������²�Ʒ����·���ó��н����������ۣ���֪�ò�Ʒÿ���������
����Ϊ�˵��������²�Ʒ����·���ó��н����������ۣ���֪�ò�Ʒÿ���������![]() ��
��![]() ��ÿ�������ۼ�
��ÿ�������ۼ�![]() Ԫ
Ԫ![]() ��
��![]() ֮�������¹�ϵ��
֮�������¹�ϵ��![]()
![]() ��д���ó����������ֲ�Ʒÿ�����������
��д���ó����������ֲ�Ʒÿ�����������![]() Ԫ
Ԫ![]() ��x֮��ĺ�����ϵʽ������������ܻ�ȡ����������Ƕ���Ԫ��
��x֮��ĺ�����ϵʽ������������ܻ�ȡ����������Ƕ���Ԫ��
![]() ���������ȡ1500Ԫ������
���������ȡ1500Ԫ������![]() ��ÿ�������ۼۣ�
��ÿ�������ۼۣ�
![]() ���������ȡ��������1500Ԫ�������ÿ�������ۼ�X�ķ�Χ��
���������ȡ��������1500Ԫ�������ÿ�������ۼ�X�ķ�Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺��һ�������������y1��y2������xȡͬһ��ֵ��ʹ��y1��y2����ô��y1��y2Ϊ���������������ƶ�Ӧx��ֵΪy1��y2�ġ������㡱��
�����������������Ϊy1��y2Ϊ����������������ôy1+y2�����ֵ��Ϊy1��y2�ġ���Ӯֵ����
��1���жϺ���y��x+2m��y��![]() �Ƿ�Ϊ������������������ǣ������m��1ʱ���ǵĺ����㣻������ǣ���˵�����ɣ�
�Ƿ�Ϊ������������������ǣ������m��1ʱ���ǵĺ����㣻������ǣ���˵�����ɣ�
��2���жϺ���y��x+2m��y��3x��1��|x|��2���Ƿ�Ϊ������������������ǣ�����������㣻������ǣ���˵�����ɣ�
��3����֪����y��x+2m��y��x2����2m+1��x+��m2+4m��3����0��x��5���ǡ�����������������Ψһ�����㣮
�����m��ȡֵ��Χ��
�������ǵġ���Ӯֵ��Ϊ24�������m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1�dz�����ģ�ͣ��ⳤ��ͼ��ʾ��ͼ2������һ�ֱ���չ��ͼ��
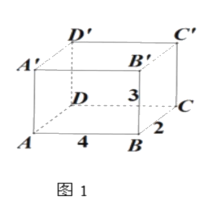
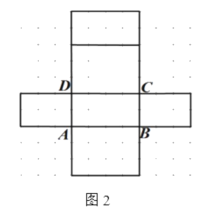

��1������ͼ2�У���ʾ��C���ܵ�λ�ã�
����ͼ3�л����������һ��չ��ͼ����ͬ��ͼ2����
��2��ͼ1�У�һֻ�ڶ���A�����ϣ�Ҫ�Ե�C������ʳ�������س�����������е���̾��룻
��3�� ������AB+BC+BB=9�������£���ABΪ��ֵʱ�����ϴ�A�س�����������е�C������̣���д�����е�һ�ַ�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com