
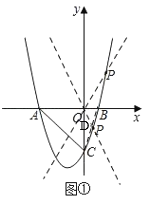
【题目】如图①,抛物线y=x2﹣(a+1)x+a与x轴交于A、B两点(点A位于点B的左侧),与y轴交于点C.已知△ABC的面积为6.
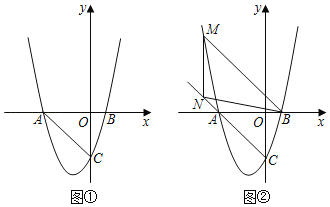
(1)求这条抛物线相应的函数表达式;
(2)在抛物线上是否存在一点P,使得∠POB=∠CBO,若存在,请求出点P的坐标;若不存在,请说明理由;
(3)如图②,M是抛物线上一点,N是射线CA上的一点,且M、N两点均在第二象限内,A、N是位于直线BM同侧的不同两点.若点M到x轴的距离为d,△MNB的面积为2d,且∠MAN=∠ANB,求点N的坐标.
【答案】(1)y=x2+2x﹣3;(2)存在,点P坐标为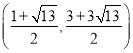 或
或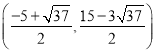 ;(3)点N的坐标为(﹣4,1)
;(3)点N的坐标为(﹣4,1)
【解析】
(1)分别令y=0 ,x=0,可表示出A、B、C的坐标,从而表示△ABC的面积,求出a的值继而即可得二次函数解析式;
(2)如图①,当点P在x轴上方抛物线上时,平移BC所在的直线过点O交x轴上方抛物线于点P,则有BC∥OP,此时∠POB=∠CBO,联立抛物线得解析式和OP所在直线的解析式解方程组即可求解;当点P在x轴下方时,取BC的中点D,易知D点坐标为(![]() ,
,![]() ),连接OD并延长交x轴下方的抛物线于点P,由直角三角形斜边中线定理可知,OD=BD,∠DOB=∠CBO即∠POB=∠CBO,联立抛物线的解析式和OP所在直线的解析式解方程组即可求解.
),连接OD并延长交x轴下方的抛物线于点P,由直角三角形斜边中线定理可知,OD=BD,∠DOB=∠CBO即∠POB=∠CBO,联立抛物线的解析式和OP所在直线的解析式解方程组即可求解.
(3)如图②,通过点M到x轴的距离可表示△ABM的面积,由S△ABM=S△BNM,可证明点A、点N到直线BM的距离相等,即AN∥BM,通过角的转化得到AM=BN,设点N的坐标,表示出BN的距离可求出点N.
(1)当y=0时,x2﹣(a+1)x+a=0,
解得x1=1,x2=a,
当x=0,y=a
∴点C坐标为(0,a),
∵C(0,a)在x轴下方
∴a<0
∵点A位于点B的左侧,
∴点A坐标为(a,0),点B坐标为(1,0),
∴AB=1﹣a,OC=﹣a,
∵△ABC的面积为6,
∴![]() ,
,
∴a1=﹣3,a2=4(因为a<0,故舍去),
∴a=﹣3,
∴y=x2+2x﹣3;
(2)设直线BC:y=kx﹣3,则0=k﹣3,
∴k=3;
①当点P在x轴上方时,直线OP的函数表达式为y=3x,
则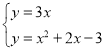 ,
,
∴ ,
,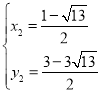 ,
,
∴点P坐标为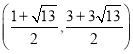 ;
;
②当点P在x轴下方时,直线OP的函数表达式为y=﹣3x,
则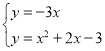
∴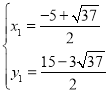 ,
,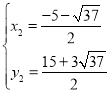 ,
,
∴点P坐标为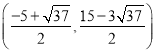 ,
,
综上可得,点P坐标为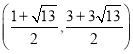 或
或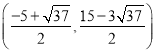 ;
;
(3)如图,过点A作AE⊥BM于点E,过点N作NF⊥BM于点F,设AM与BN交于点G,延长MN与x轴交于点H;
∵AB=4,点M到x轴的距离为d,
∴S△AMB=![]()
∵S△MNB=2d,
∴S△AMB=S△MNB,
∴![]() ,
,
∴AE=NF,
∵AE⊥BM,NF⊥BM,
∴四边形AEFN是矩形,
∴AN∥BM,
∵∠MAN=∠ANB,
∴GN=GA,
∵AN∥BM,
∴∠MAN=∠AMB,∠ANB=∠NBM,
∴∠AMB=∠NBM,
∴GB=GM,
∴GN+GB=GA+GM即BN=MA,
在△AMB和△NBM中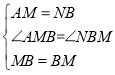
∴△AMB≌△NBM(SAS),
∴∠ABM=∠NMB,
∵OA=OC=3,∠AOC=90°,
∴∠OAC=∠OCA=45°,
又∵AN∥BM,
∴∠ABM=∠OAC=45°,
∴∠NMB=45°,
∴∠ABM+∠NMB=90°,
∴∠BHM=90°,
∴M、N、H三点的横坐标相同,且BH=MH,
∵M是抛物线上一点,
∴可设点M的坐标为(t,t2+2t﹣3),
∴1﹣t=t2+2t﹣3,
∴t1=﹣4,t2=1(舍去),
∴点N的横坐标为﹣4,
可设直线AC:y=kx﹣3,则0=﹣3k﹣3,
∴k=﹣1,
∴y=﹣x﹣3,
当x=﹣4时,y=﹣(﹣4)﹣3=1,
∴点N的坐标为(﹣4,1).



科目:初中数学 来源: 题型:
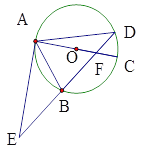
【题目】如图,已知⊙O的直径AC与弦BD相交于点F,点E是DB延长线上的一点,∠EAB=∠ADB;
(1)求证:AE是⊙O的切线;
(2)已知点B是EF的中点,求证:△EAF∽△CBA
(3)已知AF=4,CF=2,在(2)的条件下,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
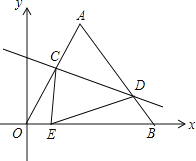
【题目】如图坐标系中,O(0,0),A(3,3![]() ),B(6,0),将△OAB沿直线CD折叠,使点A恰好落在线段OB上的点E处,若OE=
),B(6,0),将△OAB沿直线CD折叠,使点A恰好落在线段OB上的点E处,若OE=![]() ,则AC:AD的值是( )
,则AC:AD的值是( )
A.1:2B.2:3C.6:7D.7:8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阿波罗尼奥斯(Apollonius of Perga,约公元前262-190年),古希腊数学家,与欧几里得,阿基米德齐名,他的著作《圆锥曲线论》是古代世界光辉的科学成果.
材料:《圆锥曲线论》里面对抛物线的定义:平面内一个动点到一个定点与一条定直线的距离之比等于1,或者说:平面内一动点到一定点与一条直线的距离相等的轨迹就是抛物线.
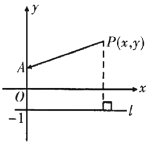
问题:已知点![]() ,
,![]() ,直线
,直线![]() ,连接
,连接![]() ,若点
,若点![]() 到直线
到直线![]() 的距离与
的距离与![]() 的长相等,请求出
的长相等,请求出![]() 与
与![]() 的关系式.
的关系式.
解:如图,∵![]() ,
,![]() ,
,
∴![]()
∵![]() ,直线
,直线![]() ,
,
∴点![]() 到直线
到直线![]() 的距离为
的距离为![]()
∵点![]() 到直线
到直线![]() 的距离与
的距离与![]() 的长相等,
的长相等,
∴![]() ,
,
平方化简得,![]() .
.
若将上述问题中![]() 点坐标改为
点坐标改为![]() ,直线
,直线![]() 变为
变为![]() ,按照问题解题思路,试求出
,按照问题解题思路,试求出![]() 与
与![]() 的关系式,并在平面直角坐标系中利用描点法画出其图象,你能发现什么?
的关系式,并在平面直角坐标系中利用描点法画出其图象,你能发现什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx﹣16的图象经过点(﹣2,﹣40)和点(6,8).
(1)求这个二次函数图象与x轴的交点坐标;
(2)当y>0时,直接写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第36届全国信息学冬令营在广州落下帷幕,长郡师生闪耀各大赛场,金牌数、奖牌数均稳居湖南省第一.学校拟预算7700元全部用于购买甲、乙、丙三种图书共20套奖励获奖师生,其中甲种图书每套500元,乙种图书每套400元,丙种图书每套250元,设购买甲种图书x套,乙种图书y套,请解答下列问题:
(1)请求出y与x的函数关系式(不需要写出自变量的取值范围);
(2)若学校购买的甲、乙两种图书共14套,求甲、乙图书各多少套?
(3)若学校购买的甲、乙两种图书均不少于1套,则有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
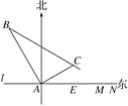
【题目】在某飞机场东西方向的地面l上有一长为1 km的飞机跑道MN(如图),在跑道MN的正西端14.5千米处有一观察站A.某时刻测得一架匀速直线降落的飞机位于点A的北偏西30°,且与点A相距15千米的B处;经过1分钟,又测得该飞机位于点A的北偏东60°,且与点A相距5![]() 千米的C处.
千米的C处.
(1)该飞机航行的速度是多少千米/小时?(结果保留根号)
(2)如果该飞机不改变航向继续航行,那么飞机能否降落在跑道MN之间?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农科所研究出一种新型的花生摘果设备,一期研发成本为每台6万元,该摘果机的销售量![]() (台)与售价
(台)与售价![]() (万元/台)之间存在函数关系:
(万元/台)之间存在函数关系:![]() .
.
(1)设这种摘果机一期销售的利润为![]() (万元),问一期销售时,在抢占市场份额(提示:销量尽可能大)的前提下利润达到32万元,此时售价为多少?
(万元),问一期销售时,在抢占市场份额(提示:销量尽可能大)的前提下利润达到32万元,此时售价为多少?
(2)由于环保局要求该机器必须增加除尘设备,科研所投入了7万元研究经费,使得环保达标且机器的研发成本每台降低了1万元,若科研所的销售战略保持不变,请问在二期销售中利润达到63万元时,该机器单台的售价为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
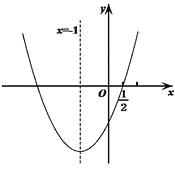
【题目】如图,二次函数![]() 的图象经过点
的图象经过点![]() ,对称轴为直线
,对称轴为直线![]() ,下列5个结论:①
,下列5个结论:①![]() ; ②
; ②![]() ; ③
; ③![]() ;④
;④![]() ; ⑤
; ⑤![]() ,其中正确的结论为________________.(注:只填写正确结论的序号)
,其中正确的结论为________________.(注:只填写正确结论的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com