练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．求下列各式中x的值．
    （1）3x=$\frac{1}{81}$；（2）（-2）x=$\frac{1}{64}$；（3）（$\frac{1}{2}$）x=16．

    分析 （1）先利用负整数指数幂的意义得到3x=3-3，然后利用底数相同，指数相等求出x的值；
    （2）先利用负整数指数幂的意义得到（-2）x=26=（-2）6，然后利用底数相同，指数相等求出x的值；
    （3）先利用负整数指数幂的意义得到2-x=24，然后利用底数相同，指数相等求出x的值．

    解答 解：（1）因为3x=3-3，
    所以x=-3；
    （2）因为（-2）x=26=（-2）6，
    所以x=6；
    （3）因为2-x=24，
    所以-x=4，即x=-4．

    点评 本题考查了负整数指数幂：a-p=1$\frac{1}{{a}^{p}}$（a≠0，p为正整数）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

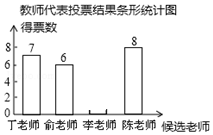    14．某校开展了“我最喜爱的老师”评选活动．确定如下评选方案：有学生和教师代表对4名候选教师进行投票，每票选1名候选教师，每位候选教师得到的教师票数的5倍与学生票数的和作为该教师的总票数．以下是根据学生和教师代表投票结果绘制的统计表和条形统计图（不完整）．
    学生投票结果统计表
    候选教师丁老师俞老师李老师陈老师
    得票数460200140300
    （1）若共有25位教师代表参加投票，则李老师得到的教师票数是多少？请补全条形统计图．（画在答案卷相对应的图上）
    （2）丁老师与李老师得到的学生总票数是600，且丁老师得到的学生票数是李老师得到的学生票数的3倍多40票，求丁老师与李老师得到的学生票数分别是多少？
    （3）在（1）、（2）的条件下，若总得票数较高的2名教师推选到市参评，你认为推选到市里的是两位老师？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．开学初，小芳和小亮去商店购买学习用品，小芳用30元钱购买钢笔的数量是小亮用25元钱购买笔记本数量的2倍，已知每支钢笔的价格比每本笔记本的价格少2元．
    （1）求每支钢笔和每本笔记本各是多少元；
    （2）学校运动会后，班主任拿出200元学校奖励基金交给小芳，再次购买上述价格的钢笔和笔记本共48件作为奖品，奖励给校运动会中表现突出的同学，经双方协商，商店给出优惠是购买商品的总金额超出50的部分给打9折，请问小芳至少要买多少支钢笔？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．将直角三角形ABC沿CB方向平移BE的距离后，得到直角三角形DEF，已知AG=4，BE=6，DE=12，求阴影部分的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．在数学活动课上，老师和同学们判断一个四边形门框是否为矩形，下面是一个学习小组拟定的方案：①测量对角线是否互相平分；②测量两组对边是否分别相等；③测量对角线是否分别相等；④测量其中三个角是否都为直角，其中，错误的方案是①②③．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．求下列各式中的x的值．
    （1）4（x-1）2-16=0；
    （2）8（2x+1）2-1=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．如果一个自然数能表示为两个自然数的平方差，那么称这个自然数为智慧数，例如：16=52-32，16就是一个智慧数，小明和小王对自然数中的智慧数迸行了如下的探索：
    小明的方法是一个一个找出来的：
    0=02-02，1=12-02，3=22-12，
    4=22-02，5=32-22，7=42-32，
    8=32-12，9=52-42，11=62-52，…
    小王认为小明的方法太麻烦，他想到：
    设k是自然数，由于（k+1）2-k2=（k+1+k）（k+1-k）=2k+1．
    所以，自然中所有奇数都是智慧数．
    问题：（1）根据上述方法，自然数中第12个智慧数是15．
    （2）他们发现0，4，8是智慧数，由此猜测4k（k≥3且k为正整数）都是智慧数，请你参考小王的办法证明4k（k≥3且k为正整数）都是智慧数．
    （3）他们还发现2，6，10都不是智慧数，由此猜测4k+2（k为自然数）都不是智慧数，请利用所学的知识判断26是否是智慧数，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．随着通讯事业的日益发达，信息传播越来越快捷．一条信息经一人转发后，收到信息的人中有$\frac{1}{3}$会将其转发给其它没有此信息的人，如果经过两轮转发后，共有331人收到此信息．
    （1）平均每人每轮转发给几个人？
    （2）若要使收到信息的人数超过3万人，需要经过几轮转发？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

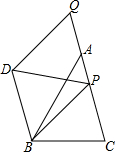    7．如图，在△ABC中，AB=6，tan∠BAC=$\frac{3}{4}$，点P为AC边上任意一点，点Q为CA延长线上任意一点，以PB、PQ为两边作?PQDB，则对角线PD的最小值为$\frac{18}{5}$．

    查看答案和解析>>

    同步练习册答案