
【题目】如图,在平面直角坐标系xOy中,已知正比例函数![]() 与一次函数
与一次函数![]() 的图象交于点A.
的图象交于点A.
(1)求点A的坐标;
(2)设x轴上有一点P(a,0),过点P作x轴的垂线(垂线位于点A的右侧),分别交![]() 和
和![]() 的图象于点B、C,连接OC.若BC=
的图象于点B、C,连接OC.若BC=![]() OA,求△OBC的面积.
OA,求△OBC的面积.

【答案】(1)A(4,3);(2)28.
【解析】
试题分析:(1)联立两一次函数的解析式求出x、y的值即可得出A点坐标;
(2)过点A作x轴的垂线,垂足为D,在Rt△OAD中根据勾股定理求出OA的长,故可得出BC的长,根据P(a,0)可用a表示出B、C的坐标,故可得出a的值,由三角形的面积公式即可得出结论.
试题解析:(1)∵由题意得,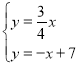 ,解得:
,解得:![]() ,∴A(4,3);
,∴A(4,3);
(2)过点A作x轴的垂线,垂足为D,在Rt△OAD中,由勾股定理得,OA=![]() =
=![]() =5,
=5,
∴BC=![]() OA=
OA=![]() ×5=7.∵P(a,0),∴B(a,
×5=7.∵P(a,0),∴B(a,![]() ),C(a,﹣a+7),∴BC=
),C(a,﹣a+7),∴BC=![]() =
=![]() ,∴
,∴![]() =7,解得a=8,∴S△OBC=
=7,解得a=8,∴S△OBC=![]() BCOP=
BCOP=![]() ×7×8=28.
×7×8=28.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】计算
(1)﹣8﹣12+2
(2)﹣18+(﹣7.5)﹣(﹣31)﹣12.5
(3)﹣ ![]() ﹣(+1
﹣(+1 ![]() )﹣(﹣
)﹣(﹣ ![]() )﹣(+4
)﹣(+4 ![]() )
)
(4)1﹣[(﹣1)﹣( ![]() )﹣(+5)﹣(
)﹣(+5)﹣( ![]() )]+|﹣4|.
)]+|﹣4|.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料并解决有关问题:我们知道|x|= 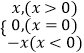 ,
,
所以当x>0时, ![]() =
= ![]() =1; 当x<0时,
=1; 当x<0时, ![]() =
= ![]() =﹣1.现在我们可以用这个结论来解决下面问题:
=﹣1.现在我们可以用这个结论来解决下面问题:
(1)已知a,b是有理数,当ab≠0时, ![]() +
+ ![]() =;
=;
(2)已知a,b是有理数,当abc≠0时, ![]() +
+ ![]() +
+ ![]() =;
=;
(3)已知a,b,c是有理数,a+b+c=0,abc<0,则 ![]() +
+ ![]() +
+ ![]() = .
= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某玩具厂熟练工人工资为:每月底薪700元,加奖励工资按件计算,一个月工作日为25天,每天工作8小时,加工1件A种玩具计酬10元,加工1件B种玩具计酬8元.在工作中发现一名熟练工人加工1件A种玩具和2件B种玩具需4小时,加工3件A种玩具和1件B种玩具需7小时.(工人月工资=底薪+计件工资)
(1)求熟练工人每加工一件A种玩具和一件B种玩具,分别需要多少时间?
(2)深圳市规定最低工资标准为每月2030元,但玩具厂规定:“每名工人每月必须加工A、B两种工具,且加工A种玩具数量不少于B种玩具的一半”.若设一名熟练工人每月加工A种玩具a件,工资总额为w元,请你运用所学知识判断该公司在执行规定后是否违背了深圳市最低工资标准?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=∠C=45°,点D在BC边上,点E在AC边上,且∠ADE=∠AED,连结DE. 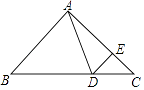
(1)当∠BAD=60°,求∠CDE的度数;
(2)当点D在BC(点B、C除外)边上运动时,试写出∠BAD与∠CDE的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于点E;
(1)若B、C在DE的同侧(如图所示)且AD=CE.求证:AB⊥AC; 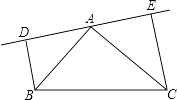
(2)若B、C在DE的两侧(如图所示),其他条件不变,AB与AC仍垂直吗?若是请给出证明;若不是,请说明理由. 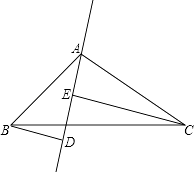
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设[a]表示不超过a的最大整数,如[4.3]=4,[-4.3]=-5,则下列各式中正确的是( )
A. [a]=|a| B. [a]=|a|-1 C. [a]=-a D. [a]>a-1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个直角∠AOB,∠COD有相同的顶点O,下列结论:①∠AOC=∠BOD;
②∠AOC+∠BOD=90°;③若OC平分∠AOB,则OB平分∠COD;④∠AOD的平分线与∠COB的平分线是同一条射线. 其中正确的个数有( )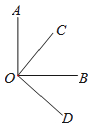
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com