
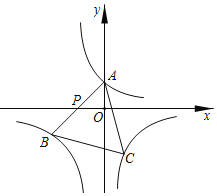
【题目】如图,将反比例函数y=![]() (k>0)的图象向左平移2个单位长度后记为图象c,c与y轴相交于点A,点P为x轴上一点,点A关于点P的对称点B在图象c上,以线段AB为边作等边△ABC,顶点C恰好在反比例函数y=﹣
(k>0)的图象向左平移2个单位长度后记为图象c,c与y轴相交于点A,点P为x轴上一点,点A关于点P的对称点B在图象c上,以线段AB为边作等边△ABC,顶点C恰好在反比例函数y=﹣![]() (x>0)的图象上,则k=_____.
(x>0)的图象上,则k=_____.
 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】关于三角函数有如下的公式:
①cos(α+β)=cosαcosβ﹣sinαsinβ;sin(α+β)=sinαcosβ+cosαsinβ;
②tan(α+β)=![]() .
.
③利用这些公式可以将一些不是特殊角的三角函数转化为特殊角的三角函数来求值,如tan105°=tan(45°+60°)=![]() =
=![]() =
=![]() =
=![]() =
=![]() .
.
根据上面的知识,你可以选择适当的公式解决下面的实际问题:
(1)求cos75°的值;
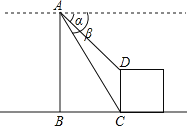
(2)如图,直升机在一建筑物CD上方的点A处测得建筑物顶端点D的俯角α为60°,底端点C的俯角β为75°,此时直升机与建筑物CD的水平距离BC为42m,求建筑物CD的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
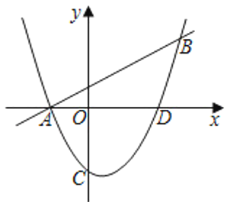
【题目】如图,一次函数y=![]() x+1的图象与二次函数y=
x+1的图象与二次函数y=![]() x2+bx+c的图象交于A,B两点,点A在x轴上.点B的横坐标为4.
x2+bx+c的图象交于A,B两点,点A在x轴上.点B的横坐标为4.
(1)b= ,c= ;
(2)设二次函数的图象与y轴交于C点,与x轴的另一个交点为D.连接AC,CD,求∠ACD的正弦值;
(3)若M点在x轴下方二次函数图象上,
①过M点作y轴平行线交直线AB于点E,以M点为圆心,ME的长为半径画圆,求圆M在直线AB上截得的弦长的最大值;
②若∠ABM=∠ACO,则点M的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着《流浪地球》的热播,其同名科幻小说的销量也急剧上升.为应对这种变化,某网店分别花20000元和30000元先后两次增购该小说,第二次的数量比第一次多500套,且两次进价相同.
(1)该科幻小说第一次购进多少套?
(2)根据以往经验:当销售单价是25元时,每天的销售量是250套;销售单价每上涨1元,每天的销售量就减少10套.网店要求每套书的利润不低于10元且不高于18元.
①直接写出网店销售该科幻小说每天的销售量y(套)与销售单价x(元)之间的函数关系式及自变量x的取值范围;
②网店决定每销售1套该科幻小说,就捐赠a(0<a<7)元给困难职工,每天扣除捐赠后可获得的最大利润为1960元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
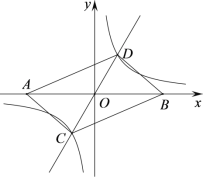
【题目】如图,在平面直角坐标系中,点A的坐标为(m,0),m<0,点B与点A 关于原点对称,直线![]() 与双曲线
与双曲线![]() 交于C,D两点.
交于C,D两点.
(1)直接判断后填空:四边形ACBD的形状一定是 ;
(2)若点D(1,t),求双曲线的解析式;
(3)在(2)的前提下,四边形ACBD为矩形时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
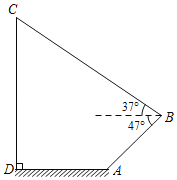
【题目】如图,一架无人机在距离地面高度为21.4米的点B处,测得地面点A的俯角为47°,接着,这架无人机从点B沿仰角为37°的方向继续飞行20![]() 米到达点C,此时测得点C恰好在地面点D的正上方,且A,D两点在同一水平线上,求A,D两点之间的距离.(结果精确到1米;参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin47°≈0.73,cos47°≈0.68,tan47°≈1.07,
米到达点C,此时测得点C恰好在地面点D的正上方,且A,D两点在同一水平线上,求A,D两点之间的距离.(结果精确到1米;参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin47°≈0.73,cos47°≈0.68,tan47°≈1.07,![]() ≈2.45)
≈2.45)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲乙两个玩具小汽车在笔直的240米跑道![]() 上进行折返跑游戏,甲从点
上进行折返跑游戏,甲从点![]() 出发,匀速在
出发,匀速在![]() 、
、![]() 之间折返跑,同时乙从点
之间折返跑,同时乙从点![]() 出发,以大于甲的速度匀速在
出发,以大于甲的速度匀速在![]() 、
、![]() 之间折返跑.在折返点的时间忽略不计.
之间折返跑.在折返点的时间忽略不计.

(1)若甲的速度为![]() ,乙的速度为
,乙的速度为![]() ,第一次迎面相遇的时间为
,第一次迎面相遇的时间为![]() ,则
,则![]() 与
与![]() 的关系式___________;
的关系式___________;
(注释:当两车相向而行时相遇是迎面相遇,当两车在![]() 点相遇时也视为迎面相遇)
点相遇时也视为迎面相遇)
(2)如图1,
①若甲乙两车在距![]() 点20米处第一次迎面相遇,则他们在距
点20米处第一次迎面相遇,则他们在距![]() 点_______米第二次迎面相遇:
点_______米第二次迎面相遇:
②若甲乙两车在距![]() 点50米处第一次迎面相遇,则他们在距
点50米处第一次迎面相遇,则他们在距![]() 点__________米第二次迎面相遇;
点__________米第二次迎面相遇;
(3)设甲乙两车在距![]() 点
点![]() 米处第一次迎面相遇,在距
米处第一次迎面相遇,在距![]() 点
点![]() 米处第二次迎面相遇.某同学发现了
米处第二次迎面相遇.某同学发现了![]() 与
与![]() 的函数关系,并画出了部分函数图象(线段
的函数关系,并画出了部分函数图象(线段![]() ,不包括点
,不包括点![]() ,如图2所示).
,如图2所示).
①则![]() _______,并在图2中补全
_______,并在图2中补全![]() 与
与![]() 的函数图象(在图中注明关键点的数据);
的函数图象(在图中注明关键点的数据);
②分别求出各部分图象对应的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】文化是一个国家、一个民族的灵魂,近年来,央视推出《中国诗词大会》、《中国成语大会》、《朗读者》、《经曲咏流传》等一系列文化栏目.为了解学生对这些栏目的喜爱情况,某学校组织学生会成员随机抽取了部分学生进行调查,被调查的学生必须从《经曲咏流传》(记为A)、《中国诗词大会》(记为B)、《中国成语大会》(记为C)、《朗读者》(记为D)中选择自己最喜爱的一个栏目,也可以不选以上四类而写出一个自己最喜爱的其他文化栏目(这时记为E).根据调查结果绘制成如图所示的两幅不完整的统计图.
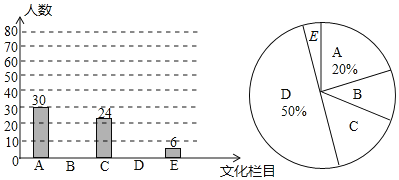
请根据图中信息解答下列问题:
(1)在这项调查中,共调查了 名学生;
(2)最喜爱《朗读者》的学生有 名;
(3)扇形统计图中“B”所在扇形圆心角的度数为 ;
(4)选择“E”的学生中有2名女生,其余为男生,现从选择“E”的学生中随机选出两名学生参加座谈,请直接写出:刚好选到一名男生和一名女生的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习《圆》这一单元时,我们学习了圆周角定理的推论:圆内接四边形的对角互补;事实上,它的逆命题:对角互补的四边形的四个顶点共圆,也是一个真命题.在图形旋转的综合题中经常会出现对角互补的四边形,那么,我们就可以借助“对角互补的四边形的四个顶点共圆”,然后借助圆的相关知识来解决问题,例如:
已知:![]() 是等边三角形,点
是等边三角形,点![]() 是
是![]() 内一点,连接
内一点,连接![]() ,将线段
,将线段![]() 绕
绕![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,并延长
,并延长![]() 交
交![]() 于点
于点![]() .当点
.当点![]() 在如图所示的位置时:
在如图所示的位置时:
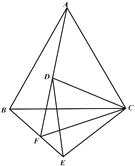
(1)观察填空:
①与![]() 全等的三角形是________;
全等的三角形是________;
②![]() 的度数为
的度数为
(2)利用题干中的结论,证明:![]() ,
,![]() ,
,![]() ,
,![]() 四点共圆;
四点共圆;
(3)直接写出线段![]() ,
,![]() ,
,![]() 之间的数量关系.____________________.
之间的数量关系.____________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com