
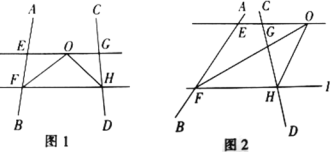
【题目】[探究]如图,∠AFH和∠CHF的平分线交于点O,EG经过点O且平行于FH,分别与AB,CD交于点E、G.
(1)若∠AFH=60°,∠CHF=50°,则∠EOF= °,∠ FOH= °
(2)若∠AFH+∠CHF= 100°,求∠FOH的度数.
(3)当∠FOH=_____ °时 ,AB//CD.
[拓展]如图,∠AFH和∠CHI的平分线交于点O,EG经过点O且平行于FH,分别与AB,CD交于点E、G.若∠AFH+∠CHF=a,求∠FOH的度数. (用含a的代数式表示)
【答案】(1)30,125;(2) 130°;(3)90°;拓展: 90°-![]() a.
a.
【解析】
(1)依据角平分线以及平行线的性质,即可得到∠EOF的度数,依据三角形内角和定理,即可得到∠FOH的度数;(2)依据角平分线以及平行线的性质、三角形内角和定理,即可得到∠FOH的度数; (3) 因为∠OFH=![]() ∠AFH,∠OHF=
∠AFH,∠OHF=![]() ∠CHF,所以∠OFH+∠CHF=
∠CHF,所以∠OFH+∠CHF=![]() (∠AFH+∠CHF),当∠AFH+∠CHF=180°时,AB//CD,此时 ∠OFH+∠CHF=
(∠AFH+∠CHF),当∠AFH+∠CHF=180°时,AB//CD,此时 ∠OFH+∠CHF=![]() (∠AFH+∠CHF)=
(∠AFH+∠CHF)=![]() ×180°=90° ,根据三角形内角和得:∠FOH=180°-(∠OFH+∠CHF )=90°.
×180°=90° ,根据三角形内角和得:∠FOH=180°-(∠OFH+∠CHF )=90°.
【拓展】根据∠AFH和∠CHI的平分线交于点O,可得∠OFH=![]() ∠AFH,∠OHI=
∠AFH,∠OHI=![]() ∠CHI,再根据∠FOH=∠OHI-∠OFH进行计算,即可得到∠FOH的度数.
∠CHI,再根据∠FOH=∠OHI-∠OFH进行计算,即可得到∠FOH的度数.
解,【探究】(1) )∵∠AFH=60°,OF平分∠AFH,
∴∠OFH=30°,
又∵EG∥FH,
∴∠EOF=∠OFH=30°;
∵∠CHF=50°,OH平分∠CHF,
∴∠FHO=25°,
∴△FOH中,∠FOH=180°-∠OFH-∠OHF=125°;
故答案为:30,125.
(2)因为FO平分∠AFH,HO平分∠CHF. 所以∠OFH=![]() ∠AFH,∠OHF=
∠AFH,∠OHF=![]() ∠CHF.
∠CHF.
因为∠AFH+∠CHF=100°,所以∠OFH+∠OHF=![]() (∠AFH+∠CHF)=50°
(∠AFH+∠CHF)=50°
∵EG∥FH,
∴∠EOF=∠OFH,∠GOH=∠OHF.
∴∠EOF+∠GOH=∠OFH+∠OHF=50°.
∵∠EOF+∠GOH+∠FOH=180°,
所以∠FOH= 180°-(∠OFH+∠OHF)=180°-50°![]() =130°.
=130°.
(3) ∵∠OFH=![]() ∠AFH,∠OHF=
∠AFH,∠OHF=![]() ∠CHF,
∠CHF,
∴∠OFH+∠CHF=![]() (∠AFH+∠CHF),
(∠AFH+∠CHF),
当∠AFH+∠CHF=180°时,AB//CD,此时 ∠OFH+∠CHF=![]() (∠AFH+∠CHF)=
(∠AFH+∠CHF)=![]() ×180°=90° ,根据三角形内角和得:∠FOH=180°-(∠OFH+∠CHF )=90°.
×180°=90° ,根据三角形内角和得:∠FOH=180°-(∠OFH+∠CHF )=90°.
【拓展】
因为∠AFH和∠CHI的平分线交干点O.
所以∠OFH=![]() ∠AFH,∠OHI=
∠AFH,∠OHI=![]() ∠CHI.
∠CHI.
因为EG//FH,所以∠EOH=∠OHI,∠EOF=∠OFH.
因为∠FOH=∠EOH-∠EOF,∠FOH=∠OHI-∠EOH=![]() (∠CHI-∠AFH)=90°-
(∠CHI-∠AFH)=90°-![]() a.
a.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
【题目】如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进30海里到达B点,此时,测得海岛C位于北偏东30°的方向,求海岛C到航线AB的距离CD的长(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于点P(x,y),若点Q的坐标为(ax+y,x+ay),其中a为常数,则称点Q是点P的“a级关联点”例如,点P(1,4)的“3级美联点”为Q(3![]() +4,1+3
+4,1+3![]() ),即Q(7,13).
),即Q(7,13).
(1)已知点A(一2,6)的“![]() 级关联点”是点
级关联点”是点![]() ,求点
,求点![]() 的坐标。
的坐标。
(2)已知点M(m一1,2m)的“一3级关联点”M’位于y轴上.求点M’的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年南方某地发生特大洪灾,政府为了尽快搭建板房安置灾民,给某厂下达了生产A种板材48000㎡和B种板材24000㎡的任务.
⑴如果该厂安排210人生产这两种材,每人每天能生产A种板材60㎡或B种板材40㎡,请问:应分
别安排多少人生产A种板材和B种板材,才能确保同时完成各自的生产任务?
⑵某灾民安置点计划用该厂生产的两种板材搭建甲、乙两种规格的板房共400间,已知建设一间甲型板房和一间乙型板房所需板材及安置人数如下表所示:
板房 | A种板材(m2) | B种板材(m2) | 安置人数 |
甲型 | 108 | 61 | 12 |
乙型 | 156 | 51 | 10 |
问这400间板房最多能安置多少灾民?
查看答案和解析>>
科目:初中数学 来源: 题型:
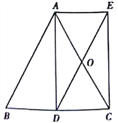
【题目】如图,AD是等腰△ABC底边BC上的高,点O是AC中点,延长DO到E
使AE∥BC,连接AE。
(1)求证:四边形ADCE是矩形;
(2)①若AB=17,BC=16,则四边形ADCE的面积= ;
②若AB=10,则BC= 时,四边形ADCE是正方形。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,河的两岸l1与l2相互平行,A,B是l1上的两点,C,D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C、D两点间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】假期,某校为了勤工俭学,要完成整个A小区的绿化工作,开始由七年级单独工作了4天,完成整个绿化工作的三分之一,这时九年级也参加工作,两个年级又共同工作了2天,才全部完成整个绿化工作,则由九年级单独完成整个绿化工作需要____天.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com