
【题目】在等腰![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,点
,点![]() 分别是
分别是![]() 轴,
轴,![]() 轴上两个动点,直角边
轴上两个动点,直角边![]() 交
交![]() 轴于点
轴于点![]() ,斜边
,斜边![]() 交
交![]() 轴于点
轴于点![]() .
.
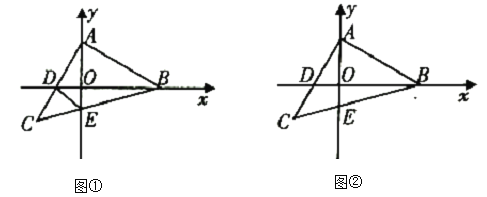
(1)如图①,当等腰![]() 运动到使点
运动到使点![]() 恰为
恰为![]() 中点时,连接
中点时,连接![]() ,求证:
,求证:![]() ;
;
(2)如图②,当等腰![]() 运动到使
运动到使![]() 时,
时,![]() 点的横坐标为
点的横坐标为![]() ,
,![]() .在
.在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 为等腰三角形?若存在,请直接写出点
为等腰三角形?若存在,请直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
【答案】(1)证明见解析;(2)存在,P点的坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)过点C作CG⊥AC交y轴于点G,则△ACG≌△ABD(ASA),即得CG=AD=CD,∠ADB=∠AGC,由∠DCE=∠GCE=45°,可证△DCE≌△GCE(SAS)得∠CDE=∠AGC,从而得到结论;
(2)根据含30°的直角三角形的特点解直角三角形,分别求出OA和AB,然后设P(a,0)分情况讨论即可.
解:(1)证明:如图,过点C作CG⊥AC交y轴于点G,
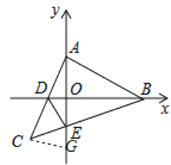
∵D为AC的中点,
∴AD=CD,
∵AC=AB,![]() ,
,
∴∠ACB=∠ABC=45°,
∵CG⊥AC ,
∴∠ACG=90°,∠CAG+∠AGC=90°,
∵∠AOD=90°,
∴∠ADO+∠DAO=90°,
∴∠AGC=∠ADO,
在△ACG和△ABD中,
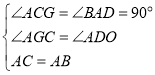
∴△ACG≌△ABD(AAS),
∴CG=AD=CD,∠ADB=∠AGC,
∵∠ACB=45°,∠ACG=90°,
∴∠DCE=∠GCE=45°,
在△DCE和△GCE中,
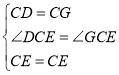
∴△DCE≌△GCE(SAS),
∴∠CDE=∠AGC,
∴∠ADB=∠CDE;
(2)存在,
∵![]() ,
,![]() ,
,
∴![]() ,即
,即![]() ,
,
∴在Rt△AOB中根据勾股定理![]() ,
,
即![]() ,
,
解得OA=3,AB=2OA=6,
∴![]() ,
,
设P(a,0),则![]() ,
,
①若AP=BP,则AP2=BP2,即
![]() ,解得
,解得![]()
∴![]() ,
,
②若AP=AB,则AP2=AB2,即
![]() ,解得
,解得![]() 或
或![]() (舍去),
(舍去),
∴![]() ,
,
③若AB=AB,则AB2=AB2,即
![]() ,
,
解得![]() 或
或![]() ,
,
∴![]() 或
或![]() ,
,
综上所述P点的坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】奉节脐橙是重庆市奉节县特产,中国地理标志产品,眼下,正值奉节脐橙销售旺季,某商家看准商机,第一次用4800元购进一批奉节脐橙,销售良好,于是第二次又用12000元购进一批奉节脐橙,但此时进价比第一次涨了2元,所购进的数量恰好是第一次购进数量的两倍.
(1)求第一次购进奉节脐橙的进价.
(2)实际销售中,两次售价均相同,在销售过程中,由于消费者挑选后,果品下降,第一批奉节脐橙的最后100千克八折售出,第二批奉节脐橙的最后800千克九折售出,若售完这两批奉节脐橙的获利不低于9400元,则售价至少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+b的图象经过点A(—1,—5),且与正比例函数![]() 的图象相交于点B(2,a).
的图象相交于点B(2,a).
(1)求a的值;
(2)求一次函数y=kx+b的表达式;
(3)在同一坐标系中,画出这两个函数的图象,并求这两条直线与y轴围成的三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个正整数能表示成两个连续偶数的平方差,那么称这个正整数为“巧数”,如:![]() ,
,![]() ,
,![]() ,因此4,12,20这三个数都是“巧数”.
,因此4,12,20这三个数都是“巧数”.
(1)400和2020这两个数是“巧数”吗?为什么?
(2)设两个连续偶数为![]() 和
和![]() (其中
(其中![]() 取正整数),由这两个连续偶数构造的“巧数”是4的倍数吗?为什么?
取正整数),由这两个连续偶数构造的“巧数”是4的倍数吗?为什么?
(3)求介于50到101之间所有“巧数”之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】万圣节两周前,某商店购进1000个万圣节面具,进价为每个6元,第一周以每个10元的价格售出200个;随着万圣节的临近,预计第二周若按每个10元的价格销售可售出400个,但商店为了尽快减少库存,决定单价降价x元销售![]() 根据市场调查,单价每降低1元,可多售出100个,但售价不得低于进价
根据市场调查,单价每降低1元,可多售出100个,但售价不得低于进价![]() ;节后,商店对剩余面具清仓处理,以第一周售价的四折全部售出.
;节后,商店对剩余面具清仓处理,以第一周售价的四折全部售出.
![]() 当单价降低2元时,计算第二周的销售量和售完这批面具的总利润;
当单价降低2元时,计算第二周的销售量和售完这批面具的总利润;
![]() 如果销售完这批面具共获利1300元,问第二周每个面具的销售价格为多少元?
如果销售完这批面具共获利1300元,问第二周每个面具的销售价格为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于![]() 的一元二次方程x2-4x+k+1=0
的一元二次方程x2-4x+k+1=0
(1)若![]() =-1是方程的一个根,求k值和方程的另一根;
=-1是方程的一个根,求k值和方程的另一根;
(2)设x1,x2是关于x的方程x2-4x+k+1=0的两个实数根,是否存在实数k,使得x1x2>x1+x2成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
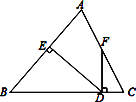
【题目】如图所示,△ABC中,AB=BC,DE⊥AB于点E,DF⊥BC于点D,交AC于F.
⑴若∠AFD=155°,求∠EDF的度数;
⑵若点F是AC的中点,求证:∠CFD=![]() ∠B.
∠B.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com