
【题目】万圣节两周前,某商店购进1000个万圣节面具,进价为每个6元,第一周以每个10元的价格售出200个;随着万圣节的临近,预计第二周若按每个10元的价格销售可售出400个,但商店为了尽快减少库存,决定单价降价x元销售![]() 根据市场调查,单价每降低1元,可多售出100个,但售价不得低于进价
根据市场调查,单价每降低1元,可多售出100个,但售价不得低于进价![]() ;节后,商店对剩余面具清仓处理,以第一周售价的四折全部售出.
;节后,商店对剩余面具清仓处理,以第一周售价的四折全部售出.
![]() 当单价降低2元时,计算第二周的销售量和售完这批面具的总利润;
当单价降低2元时,计算第二周的销售量和售完这批面具的总利润;
![]() 如果销售完这批面具共获利1300元,问第二周每个面具的销售价格为多少元?
如果销售完这批面具共获利1300元,问第二周每个面具的销售价格为多少元?
【答案】(1)当单价降低2元时,第二周的销售量为600和售完这批面具的总利润1600 ;(2) 第二周的销售价格为![]() 元.
元.
【解析】
(1)第二周的销售量=400+100x.利润=售价-成本价;
(2)根据纪念品的进价和售价以及销量分别表示出两周的总利润,进而得出等式求出即可.
(1)第二周的销售量为:400+100x=400+100x=400+100×2=600.
总利润为:200×(10-6)+(8-6)×600+200(4-6)=1600.
答:当单价降低2元时,第二周的销售量为600和售完这批面具的总利润1600;
![]() 由题意得出:200×(10-6)+(10-x-6)(400+100x)+(4-6)[(1000-200)-(400+100x)]=1300,
由题意得出:200×(10-6)+(10-x-6)(400+100x)+(4-6)[(1000-200)-(400+100x)]=1300,
整理得:x2-2x-3=0,
解得:x1=3;x2=-1(舍去),
∴10-3=7(元).
答:第二周的销售价格为7元.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们定义直线![]() 为抛物线
为抛物线![]() 、b、c为常数,
、b、c为常数,![]() 的“梦想直线”;有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“梦想三角形”.
的“梦想直线”;有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“梦想三角形”.

已知抛物线![]() 与其“梦想直线”交于A、B两点
与其“梦想直线”交于A、B两点![]() 点A在点B的左侧
点A在点B的左侧![]() ,与x轴负半轴交于点C.
,与x轴负半轴交于点C.
![]() 填空:该抛物线的“梦想直线”的解析式为______,点A的坐标为______,点B的坐标为______;
填空:该抛物线的“梦想直线”的解析式为______,点A的坐标为______,点B的坐标为______;
![]() 如图,点M为线段CB上一动点,将
如图,点M为线段CB上一动点,将![]() 以AM所在直线为对称轴翻折,点C的对称点为N,若
以AM所在直线为对称轴翻折,点C的对称点为N,若![]() 为该抛物线的“梦想三角形”,求点N的坐标;
为该抛物线的“梦想三角形”,求点N的坐标;
![]() 当点E在抛物线的对称轴上运动时,在该抛物线的“梦想直线”上,是否存在点F,使得以点A、C、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.
当点E在抛物线的对称轴上运动时,在该抛物线的“梦想直线”上,是否存在点F,使得以点A、C、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与坐标轴相交于
与坐标轴相交于![]() 、
、![]() 、
、![]() 三点,
三点,![]() 是线段
是线段![]() 上一动点(端点除外),过
上一动点(端点除外),过![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
![]() 直接写出
直接写出![]() 、
、![]() 、
、![]() 的坐标;
的坐标;
![]() 求抛物线
求抛物线![]() 的对称轴和顶点坐标;
的对称轴和顶点坐标;
![]() 求
求![]() 面积的最大值,并判断当
面积的最大值,并判断当![]() 的面积取最大值时,以
的面积取最大值时,以![]() 、
、![]() 为邻边的平行四边形是否为菱形.
为邻边的平行四边形是否为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
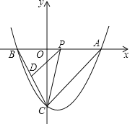
【题目】在等腰![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,点
,点![]() 分别是
分别是![]() 轴,
轴,![]() 轴上两个动点,直角边
轴上两个动点,直角边![]() 交
交![]() 轴于点
轴于点![]() ,斜边
,斜边![]() 交
交![]() 轴于点
轴于点![]() .
.
(1)如图①,当等腰![]() 运动到使点
运动到使点![]() 恰为
恰为![]() 中点时,连接
中点时,连接![]() ,求证:
,求证:![]() ;
;
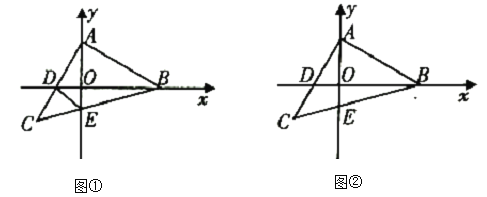
(2)如图②,当等腰![]() 运动到使
运动到使![]() 时,
时,![]() 点的横坐标为
点的横坐标为![]() ,
,![]() .在
.在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 为等腰三角形?若存在,请直接写出点
为等腰三角形?若存在,请直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理是数学史上非常重要的一个定理.早在![]() 多年以前,人们就开始对它进行研究,至今已有几百种证明方法.在欧几里得编的《原本》中证明勾股定理的方法如下,请同学们仔细阅读并解答相关问题:如图,分别以
多年以前,人们就开始对它进行研究,至今已有几百种证明方法.在欧几里得编的《原本》中证明勾股定理的方法如下,请同学们仔细阅读并解答相关问题:如图,分别以![]() 的三边为边长,向外作正方形
的三边为边长,向外作正方形![]() 、
、![]() 、
、![]() .
.
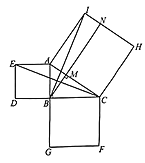
(1)连接![]() 、
、![]() ,求证:
,求证:![]()
(2)过点![]() 作
作![]() 的垂线,交
的垂线,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
①试说明四边形![]() 与正方形
与正方形![]() 的面积相等;
的面积相等;
②请直接写出图中与正方形![]() 的面积相等的四边形.
的面积相等的四边形.
(3)由第(2)题可得:正方形![]() 的面积
的面积![]() 正方形
正方形![]() 的面积
的面积![]() _______________的面积,即在
_______________的面积,即在![]() 中,
中,![]() __________________.
__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要建一个如图所示的面积为300![]() 的长方形围栏,围栏总长50m,一边靠墙(墙长25m),
的长方形围栏,围栏总长50m,一边靠墙(墙长25m),

(1)求围栏的长和宽;
(2)能否围成面积为400 ![]() 的长方形围栏?如果能,求出该长方形的长和宽,如果不能请说明理由。
的长方形围栏?如果能,求出该长方形的长和宽,如果不能请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com