
【题目】已知一次函数y=kx+b的图象经过点A(—1,—5),且与正比例函数![]() 的图象相交于点B(2,a).
的图象相交于点B(2,a).
(1)求a的值;
(2)求一次函数y=kx+b的表达式;
(3)在同一坐标系中,画出这两个函数的图象,并求这两条直线与y轴围成的三角形的面积.
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:
【题目】亚洲文明对话大会召开期间,大批的大学生志愿者参与服务工作.某大学计划组织本校全体志愿者统一乘车去会场,若单独调配36座新能源客车若干辆,则有2人没有座位;若只调配22座新能源客车,则用车数量将增加4辆,并空出2个座位.
(1)计划调配36座新能源客车多少辆?该大学共有多少名志愿者?
(2)若同时调配36座和22座两种车型,既保证每人有座,又保证每车不空座,则两种车型各需多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家商店进行门店升级需要装修,装修期间暂停营业,若请甲乙两个装修组同时施工,8天可以完成,需付费用共3520元;若先请甲组单独做6天,再请乙组单独做12天可以完成,需付费用3480元,问:
![]() 甲、乙两组工作一天,商店各应付多少钱?
甲、乙两组工作一天,商店各应付多少钱?
![]() 已知甲组单独完成需12天,乙组单独完成需24天,单独请哪个组,商店所需费用最少?
已知甲组单独完成需12天,乙组单独完成需24天,单独请哪个组,商店所需费用最少?
![]() 装修完毕第二天即可正常营业,且每天仍可盈利200元
装修完毕第二天即可正常营业,且每天仍可盈利200元![]() 即装修前后每天盈利不变
即装修前后每天盈利不变![]() ,你认为商店应如何安排施工更有利?说说你的理由
,你认为商店应如何安排施工更有利?说说你的理由![]() 可用
可用![]() 问的条件及结论
问的条件及结论![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,A、B两点的坐标分别为A(0,m)、B(n,0),且|m﹣n﹣3|+![]() =0,点P从A出发,以每秒1个单位的速度沿射线AO匀速运动,设点P的运动时间为t秒.
=0,点P从A出发,以每秒1个单位的速度沿射线AO匀速运动,设点P的运动时间为t秒.
(1)求OA、OB的长;
(2)连接PB,设△POB的面积为S,用t的式子表示S;
(3)过点P作直线AB的垂线,垂足为D,直线PD与x轴交于点E,在点P运动的过程中,是否存在这样的点P,使△EOP≌△AOB?若存在,请求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与坐标轴相交于
与坐标轴相交于![]() 、
、![]() 、
、![]() 三点,
三点,![]() 是线段
是线段![]() 上一动点(端点除外),过
上一动点(端点除外),过![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
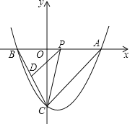
![]() 直接写出
直接写出![]() 、
、![]() 、
、![]() 的坐标;
的坐标;
![]() 求抛物线
求抛物线![]() 的对称轴和顶点坐标;
的对称轴和顶点坐标;
![]() 求
求![]() 面积的最大值,并判断当
面积的最大值,并判断当![]() 的面积取最大值时,以
的面积取最大值时,以![]() 、
、![]() 为邻边的平行四边形是否为菱形.
为邻边的平行四边形是否为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,点
,点![]() 分别是
分别是![]() 轴,
轴,![]() 轴上两个动点,直角边
轴上两个动点,直角边![]() 交
交![]() 轴于点
轴于点![]() ,斜边
,斜边![]() 交
交![]() 轴于点
轴于点![]() .
.
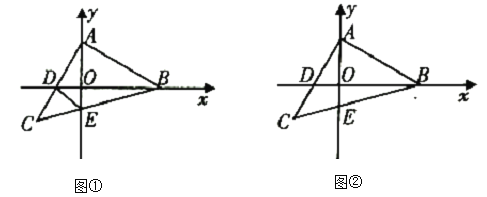
(1)如图①,当等腰![]() 运动到使点
运动到使点![]() 恰为
恰为![]() 中点时,连接
中点时,连接![]() ,求证:
,求证:![]() ;
;
(2)如图②,当等腰![]() 运动到使
运动到使![]() 时,
时,![]() 点的横坐标为
点的横坐标为![]() ,
,![]() .在
.在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 为等腰三角形?若存在,请直接写出点
为等腰三角形?若存在,请直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理是数学史上非常重要的一个定理.早在![]() 多年以前,人们就开始对它进行研究,至今已有几百种证明方法.在欧几里得编的《原本》中证明勾股定理的方法如下,请同学们仔细阅读并解答相关问题:如图,分别以
多年以前,人们就开始对它进行研究,至今已有几百种证明方法.在欧几里得编的《原本》中证明勾股定理的方法如下,请同学们仔细阅读并解答相关问题:如图,分别以![]() 的三边为边长,向外作正方形
的三边为边长,向外作正方形![]() 、
、![]() 、
、![]() .
.
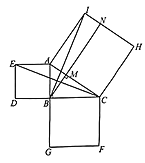
(1)连接![]() 、
、![]() ,求证:
,求证:![]()
(2)过点![]() 作
作![]() 的垂线,交
的垂线,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
①试说明四边形![]() 与正方形
与正方形![]() 的面积相等;
的面积相等;
②请直接写出图中与正方形![]() 的面积相等的四边形.
的面积相等的四边形.
(3)由第(2)题可得:正方形![]() 的面积
的面积![]() 正方形
正方形![]() 的面积
的面积![]() _______________的面积,即在
_______________的面积,即在![]() 中,
中,![]() __________________.
__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用一根长度为![]() 的细绳围成一个等腰三角形.
的细绳围成一个等腰三角形.
(1)如果所围等腰三角形的腰长是底边长的2倍,则此时的底边长度是多少?
(2)所围成的等腰三角形的腰长不可能等于![]() ,请简单说明原因.
,请简单说明原因.
(3)若所围成的等腰三角形的腰长为![]() ,请求出
,请求出![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com