
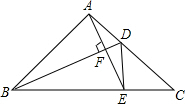
 如图,在△ABC中,BD是角平分线,AB=AC=5,BC=8,过A作AE⊥BD交于F,交BC于E,连结DE,则S△ABF:S△CDE=$\frac{65}{48}$.
如图,在△ABC中,BD是角平分线,AB=AC=5,BC=8,过A作AE⊥BD交于F,交BC于E,连结DE,则S△ABF:S△CDE=$\frac{65}{48}$. 分析 过A作AM⊥BC于M,过E作EN⊥AC于N,根据等腰三角形的性质得到BM=CM=4,由勾股定理得到AM=$\sqrt{A{B}^{2}-B{M}^{2}}$=3,推出△ABF≌△BEF,根据全等三角形的性质得到BE=AB=5,S△ABF=$\frac{1}{2}$S△ABE=$\frac{1}{2}$×$\frac{1}{2}$×5×3=$\frac{15}{4}$,根据全等三角形的性质得到AD=DE,通过△CEN∽△AMB,求得CN=$\frac{12}{5}$.EN=$\frac{9}{5}$,根据勾股定理列方程得到CD=$\frac{40}{13}$,于是得到结论.
解答 解:过A作AM⊥BC于M,过E作EN⊥AC于N,
∵AB=AB,
∴BM=CM=4,
∴AM=$\sqrt{A{B}^{2}-B{M}^{2}}$=3,
∵BD是角平分线,
∴∠ABF=∠EBF,
∵AE⊥BD,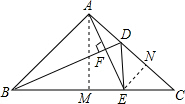
∴∠AFB=EFB=90°,
在△ABF与△BEF中,
$\left\{\begin{array}{l}{∠ABF=∠EBF}\\{BF=BF}\\{∠AFB=∠BFE}\end{array}\right.$,
∴△ABF≌△BEF,
∴BE=AB=5,S△ABF=$\frac{1}{2}$S△ABE=$\frac{1}{2}$×$\frac{1}{2}$×5×3=$\frac{15}{4}$,
∴CE=3,
在△ABD与△BED中,
$\left\{\begin{array}{l}{AB=BE}\\{∠ABD=∠EBD}\\{BD=BD}\end{array}\right.$,
∴△ABD≌△BED,
∴AD=DE,
设AD=DE=x,
∵∠ENC=∠AMB=90°,∠C=∠ABC,
∴△CEN∽△AMB,
∴$\frac{CE}{AB}=\frac{CN}{BM}=\frac{EN}{AM}$,
∴$\frac{3}{5}=\frac{CN}{4}=\frac{EN}{3}$,
∴CN=$\frac{12}{5}$.EN=$\frac{9}{5}$,
∴DN=5-x-$\frac{12}{5}$=$\frac{13}{5}$-x,
∵DE2=DN2+EN2,即x2=($\frac{13}{5}$-x)2+($\frac{9}{5}$)2,
∴x=$\frac{25}{13}$,
∴CD=$\frac{40}{13}$,
∴S△CDE=$\frac{1}{2}$×$\frac{40}{13}$×$\frac{9}{5}$=$\frac{36}{13}$,
∴S△ABF:S△CDE=$\frac{65}{48}$.
故答案为:$\frac{65}{48}$.
点评 本题考查了角平分线的性质,勾股定理,全等三角形的判定和性质,相似三角形的判定和性质,三角形的面积的计算,正确的作出辅助线是解题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB是⊙O的直径,弦CD与AB相交于点E.
如图,AB是⊙O的直径,弦CD与AB相交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,正方形ABCD和正方形DEFG的顶点在y轴上,顶点D、F在x轴上,点C在DE边上,反比例函数y=$\frac{k}{x}$(k≠0)的图象经过B,C和边EF的中点M,若S四边形ABCD=8,则正方形DEFG的面积是( )
如图,正方形ABCD和正方形DEFG的顶点在y轴上,顶点D、F在x轴上,点C在DE边上,反比例函数y=$\frac{k}{x}$(k≠0)的图象经过B,C和边EF的中点M,若S四边形ABCD=8,则正方形DEFG的面积是( )| A. | $\frac{23}{9}$ | B. | $\frac{128}{9}$ | C. | 16 | D. | $\frac{15}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
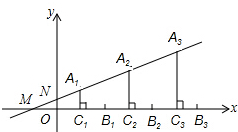 如图,直线y=$\frac{1}{2}$x+1分别与x轴、y轴交于点M,N,一组线段A1C1,A2C2,A3C3,…AnCn的端点A1,A2,A3,…An依次是直线MN上的点,这组线段分别垂直平分线段OB1,B1B2,B2,B3,…,Bn-1Bn,若OB1=B1B2=B2B3=…=Bn-1Bn=4,则点An到x轴的距离为( )
如图,直线y=$\frac{1}{2}$x+1分别与x轴、y轴交于点M,N,一组线段A1C1,A2C2,A3C3,…AnCn的端点A1,A2,A3,…An依次是直线MN上的点,这组线段分别垂直平分线段OB1,B1B2,B2,B3,…,Bn-1Bn,若OB1=B1B2=B2B3=…=Bn-1Bn=4,则点An到x轴的距离为( )| A. | 4n-4 | B. | 4n-2 | C. | 2n | D. | 2n-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 近年来,合肥“大建设”已经取得了令人瞩目的成就,今年合肥市继续重点实施综合交通、园林绿化和环境综合整治等八大类工程.如图是某建筑工地搭建的临时帐篷的横截面,其上下轮廓线分别由抛物线对称的一部分和矩形的一部分构成,最大高度为6米,底部宽度为12米,OE=3米,如果还要搭建一个矩形“支撑架”,使C、D点在抛物线上,A、B点在地面OM上,则这个“支撑架”总长L(L=AD+DC+CB)的最大值是多少?
近年来,合肥“大建设”已经取得了令人瞩目的成就,今年合肥市继续重点实施综合交通、园林绿化和环境综合整治等八大类工程.如图是某建筑工地搭建的临时帐篷的横截面,其上下轮廓线分别由抛物线对称的一部分和矩形的一部分构成,最大高度为6米,底部宽度为12米,OE=3米,如果还要搭建一个矩形“支撑架”,使C、D点在抛物线上,A、B点在地面OM上,则这个“支撑架”总长L(L=AD+DC+CB)的最大值是多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com