
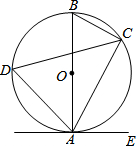
 如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.
如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.| 3 |
| 3 |
| 3 |
| 3 |
| 3 |


科目:初中数学 来源: 题型:
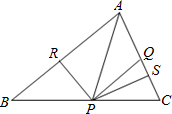 如图,在△ABC中,AQ=PQ,PR=PS,若PR⊥AB,PS⊥AC,垂足分别为点R、S,下列三个结论:①AS=AR;②QP∥AR;③△BPR≌△QPS,其中正确的是( )
如图,在△ABC中,AQ=PQ,PR=PS,若PR⊥AB,PS⊥AC,垂足分别为点R、S,下列三个结论:①AS=AR;②QP∥AR;③△BPR≌△QPS,其中正确的是( )| A、①②③ | B、① | C、①② | D、①③ |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平面直角坐标系中,直线l与x轴,y轴分别交于A,B两点,且A(4,0),B(0,3).动点P,Q同时从点O出发,点P沿着折线O→B→A匀速运动,点Q沿线段OA匀速运动,两点同时到达点A时,运动停止,已知点Q的运动速度为每秒1个单位长度.
如图,在平面直角坐标系中,直线l与x轴,y轴分别交于A,B两点,且A(4,0),B(0,3).动点P,Q同时从点O出发,点P沿着折线O→B→A匀速运动,点Q沿线段OA匀速运动,两点同时到达点A时,运动停止,已知点Q的运动速度为每秒1个单位长度.查看答案和解析>>
科目:初中数学 来源: 题型:
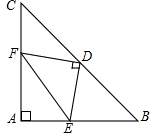 如图,在等腰Rt△ABC中,∠A=90°,AB=AC,点D是斜边BC的中点,点E、F分别为AB、AC边上的点,且DE⊥DF.
如图,在等腰Rt△ABC中,∠A=90°,AB=AC,点D是斜边BC的中点,点E、F分别为AB、AC边上的点,且DE⊥DF.查看答案和解析>>
科目:初中数学 来源: 题型:
 图,在△ABC中,D是BC边上的中点,DE⊥BC交∠BAC的平分线于点E,EF⊥AB于F,EG⊥AC的延长线于G,请你猜想BF与CG的关系,并说明为什么.
图,在△ABC中,D是BC边上的中点,DE⊥BC交∠BAC的平分线于点E,EF⊥AB于F,EG⊥AC的延长线于G,请你猜想BF与CG的关系,并说明为什么.查看答案和解析>>
科目:初中数学 来源: 题型:
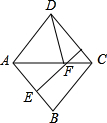 如图,在菱形ABCD中,AB的垂直平分线EF交对角线AC于点F,垂足为点E,连接DF,若∠CDF=24°,则∠DAB等于( )
如图,在菱形ABCD中,AB的垂直平分线EF交对角线AC于点F,垂足为点E,连接DF,若∠CDF=24°,则∠DAB等于( )| A、100° | B、104° |
| C、105° | D、110° |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com