
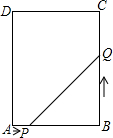
 如图,矩形ABCD中,AB=10cm,BC=20cm,两只虫子P和Q同时分别从A,B出发,沿AB,BC向B,C方形前进,虫子P每秒走1cm,虫子Q每秒走2cm,结果同时到达点B和点C.
如图,矩形ABCD中,AB=10cm,BC=20cm,两只虫子P和Q同时分别从A,B出发,沿AB,BC向B,C方形前进,虫子P每秒走1cm,虫子Q每秒走2cm,结果同时到达点B和点C.分析 (1)利用两点运动方向及速度得出BQ,BP的长,再利用勾股定理得出答案;
(2)利用当△PBQ∽△ABC时以及△QBP∽△ABC时,结合相似三角形的判定与性质得出即可.
解答 解:(1)∵两只虫子P和Q同时分别从A,B出发,沿AB,BC向B,C方形前进,虫子P每秒走1cm,虫子Q每秒走2cm,
∴都爬行4秒后,AP=4cm,BQ=8cm,
则BP=6cm,
故PQ=$\sqrt{B{P}^{2}+B{Q}^{2}}$=10(cm),
则都爬行4秒后,两虫的最短距离PQ是10厘米;
(2)设t秒时,由题意可得:BP=(10-t)cm,BQ=2tcm,
当△PBQ∽△ABC时,
则$\frac{PB}{AB}$=$\frac{BQ}{BC}$,
即$\frac{10-t}{10}$=$\frac{2t}{20}$,
解得:t=5,
当△QBP∽△ABC时,
则$\frac{QB}{AB}$=$\frac{BP}{BC}$,
即$\frac{2t}{10}$=$\frac{10-t}{20}$,
解得:t=2,
故两只蚂蚁同时出发2或5秒后,以P,B,Q为顶点的三角形与以A,B,C为顶点的三角形相似.
点评 此题主要考查了勾股定理以及相似三角形的判定与性质,正确利用分类讨论得出是解题关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5500(1+x)2=4000 | B. | 5500(1-x)2=4000 | C. | 4000(1-x)2=5500 | D. | 4000(1+x)2=5500 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{12}$ | B. | $\sqrt{{x}^{2}+2xy-{y}^{2}}$ | C. | $\sqrt{2{x}^{3}}$ | D. | $\sqrt{\frac{x}{2}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com