练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    13．已知矩形外-点P到矩形ABCD三个顶点A，B，C的距离分别为PA=60，PB=20，PC=70．求PD．

    分析 如图所示，建立直角坐标系，设矩形的长为a，宽为b，则点D（0，0），点A（a，0），点（a，b），点C（0，b），再设P（x，y），根据题意得到|PA|2、|PB|2、|PC|2、|PD|2，①+③-②得：x2+y2=8100，将⑤代入④得：|PD|2=8100．

    解答 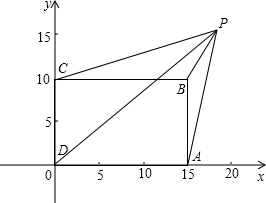解：如图所示，建立直角坐标系，设矩形的长为a，宽为b，则点D（0，0），点A（a，0），点B（a，b），点C（0，b），再设P（x，y），依据题意则有：
    |PA|2=（x-a）2+y2=3600…①
    |PB|2=（x-a）2+（y-b）2=400…②
    |PC|2=x2+（y-b）2=4900…
    |PD|2=x2+y2…④
    ①+③-②得：x2+y2=8100…⑤
    将⑤代入④得：|PD|2=8100
    解得：|PD|=90．

    点评 本题考查了勾股定理，利用勾股定理结合坐标，将线段长度表示出来是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    3．下列四个数中，最小的数是（　　）
    A．0B．1C．-$\frac{1}{2}$D．-1

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

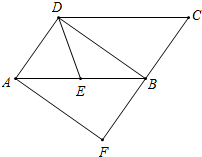    4．如图，在?ABCD中，E为边AB的中点，BD是对角线，AF∥DB交CB的延长线于F．若DE=BE，则四边形AFBD是什么特殊四边形？并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

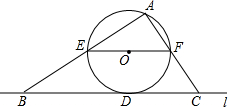    1．如图，直线L与⊙O相切于点D．过圆心O作EF∥L交⊙O于E、F两点，点A是⊙O上一点，连接AE、AF．并分别延长交直线L于 B、C两点．
    （1）求证：∠ABC+∠ACB=90°；
    （2）当⊙O的半径R=5，BD=12时，求tan∠ABC的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．以△ABC的边AB、AC为直角边分别向外作等腰直角△ABD和△ACE，M是BC的中点，N是DE的中点，连接AM、AN．
    （1）如图1，当∠BAC=90°时，其他条件不变，猜想线段BM与AN之间的数量关系，并证明你的猜想；
    （2）如图2，当∠BAC≠90°时，其他条件不变，那么（1）中猜想的结论是否成立，如果成立，请给出证明；如果不成立，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．计算过程：$\sqrt{\frac{-20}{-5}}$=$\frac{\sqrt{-5×4}}{\sqrt{-5}}$=$\frac{\sqrt{-5}×\sqrt{4}}{\sqrt{-5}}$=$\sqrt{4}$=2正确吗？如果不正确，请改正．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．计算：（3$\sqrt{72}$-12$\sqrt{\frac{1}{2}}$+$\sqrt{32}$）÷2$\sqrt{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．计算：$\sqrt{18}-\frac{2}{\sqrt{2}}$+$\sqrt{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

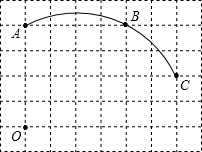    18．如图，在单位长度为1的正方形网格中，一段圆弧经过格点A、B、C．
    （1）画出该圆弧所在圆的圆心D的位置（不用写作法，保留作图痕迹），并连接AD、CD．
    （2）请在（1）的基础上，完成下列问题：
    ①以点O为原点、水平方向所在直线为x轴、竖直方向所在直线为y轴，建立平面直角坐标系，写出点的坐标：C（6，2）、D（2，0）；
    ②⊙D的半径为2$\sqrt{5}$（结果保留根号）；
    ③若用扇形ADC围成一个圆锥的侧面，则该圆锥的底面圆半径是$\frac{\sqrt{5}}{2}$；
    ④若E（7，0），试判断直线EC与⊙D的位置关系并说明你的理由．

    查看答案和解析>>

    同步练习册答案