
已知关于x的一元二次方程x2﹣6x+k+3=0有两个不相等的实数根
(1)求k的取值范围;
(2)若k为大于3的整数,且该方程的根都是整数,求k的值.
【考点】根的判别式.
【分析】(1)根据方程有两个不相等的实数根,得到根的判别式的值大于0列出关于k的不等式,求出不等式的解集即可得到k的范围;
(2)找出k范围中的整数解确定出k的值,再将k的值代入原方 程,求出方程的根,经检验即可得到满足题意的k的值.
程,求出方程的根,经检验即可得到满足题意的k的值.
【解答】解:(1)△=(﹣6)2﹣4(k+3)=36﹣4k﹣12=﹣4k+24,
∵原方程有两个不相等的实数根,
∴﹣4k+24>0.
解得 k<6;
(2)∵k<6且k为大于3的整数,
∴k=4或5.
①当k=4时,方程x2﹣6x+7=0的根不是整数.
∴k=4不符合题意;
②当k=5时,方程x2﹣6x+8=0根为x1=2,x2=4均为整数.
∴k=5符合题意.
综上所述,k的值是5.
【点评】本题考查了根的判别式,一元二次方程ax2+bx+c=0(a≠0)的根与△=b2﹣4ac有如下关系:
(1)△>0⇔方程有两个不相等的实数根;
(2)△=0⇔方程有两个相等的实数根;
(3)△<0⇔方程没有实数根.
也考查了一元二次方程的解法.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
上海世博会的某纪念品原价150元,连续两次涨价a%后售价为216元.下列所列方程中正确的是( )
A.150(1+2a%)=216 ; B.150(1+a%)2=216;
C.150(1+a%)×2=216; D.150(1+a%)+150(1+a%)2=216。
查看答案和解析>>
科目:初中数学 来源: 题型:
将抛物线向左平移2个单位,再向下平移3个单位后,所得抛物线的解析式为y=x2﹣1,则原抛物线的解析式为( )
A.y=x2+3 B.y=x2﹣3 C.y=(x+2 )2﹣3 D.y=(x﹣2)2+2
)2﹣3 D.y=(x﹣2)2+2
查看答案和解析>>
科目:初中数学 来源: 题型:
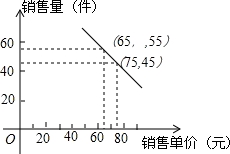
超市市场部整理出销售某品牌新款童装的销售量与销售单价的相关信息如下:
已知该童装的进价为每件60元,设销售单价为x元,销售单价不低于进价,且获利不得高于45%,设销售该款童装的利润为W元.
(1)求利润W与销售单价x之间的关系式,并求销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
(2)若超市销售该款童装获得的利润不低于500元,试确定销售单价x的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
将抛物线y=3x2向右平移两个单位,再向下平移4个单位,所得抛物线是( )
A.y=3(x+2)2+4 B.y=3(x﹣2)2+4 C.y=3(x﹣2)2﹣4 D.y=3(x+2)2﹣4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com