
【题目】如图,已知矩形 OABC,O 为坐标原点,已知 A(4,0)、C(0,2),D 为边 OA 的中点,连接 BD,M 点与 C 点重合,N 为 x 轴上一点,MN∥BD, 直线 MN 沿着 x 轴向右平移.
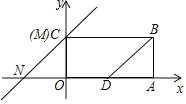
(1)当四边形 MBDN 为菱形时,N 点的坐标是 ;
(2)当 MN 平移到何处时,恰好将四边形 ODBC 的面积为 1:3 的两部分?请求出此时直线 MN 的解析式;
(3)在(1)的条件下,在矩形 OABC 的四条边上,是否存在点 F,连接 DF, 将矩形沿着 DF 所在的直线翻折,使得点 O 恰好落在直线 MN 上,若存在, 求出 F 点的坐标;若不存在,请说明理由.
【答案】(1)(2﹣2![]() ,0)或(2+2
,0)或(2+2![]() ,0);(2)y=x﹣
,0);(2)y=x﹣![]() ;(3) (0,2
;(3) (0,2![]() ﹣2)或(2
﹣2)或(2![]() ,2).
,2).
【解析】
(1)由 MN∥BD,BM∥DN,推出四边形 MNDB 是平行四边形,当 DN
=BD=2![]() 时,四边形 MNDB 是菱形;(2)分两种情形构建方程即可解决问题;
时,四边形 MNDB 是菱形;(2)分两种情形构建方程即可解决问题;
(3)如图 1﹣1 中,过 D 作 GD⊥M1N1 交 M2N2 于 H,连接 OG、OH,作线段
OG 的垂直平分线交 OC 于 F,作线段 OH 的垂直平分线交 BC 于点 F′.点 F
与点 F′即为所
(1)如图 1 中,
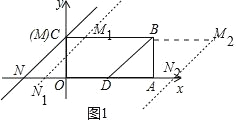
在 Rt△ABD 中,∵AD=AB=2,
∴BD= ![]() =2
=2![]() ,
,
∵MN∥BD,BM∥DN,
∴四边形 MNDB 是平行四边形,
当 DN=BD=2![]() 时,四边形 MNDB 是菱形,
时,四边形 MNDB 是菱形,
∴N(2﹣2![]() ,0)或(2+2
,0)或(2+2![]() ,0).
,0).
故答案为(2﹣2![]() ,0)或(2+2
,0)或(2+2![]() ,0).
,0).
(2)如图 2 中,设 M(m,2)
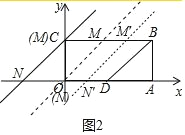
∵S 四边形 ODBC=![]() ×(2+4)×2=6.
×(2+4)×2=6.
∴当直线 MN 经过点点 O 时,S△MCN=![]() ×2×2=2=
×2×2=2=![]() S 四边形 ODBC,
S 四边形 ODBC,
∵将四边形 ODBC 的面积为 1:3 的两部分,
∴![]() m=
m=![]() ,
,
∴m=![]() 或﹣
或﹣![]() (舍弃),
(舍弃),
此时直线 MN 的解析式为 y=x+2﹣![]() ,
,
或满足:(4﹣m)2=![]() ,解得 m=
,解得 m=![]() ,
,
此时直线 MN 的解析式为 y=x﹣![]() .
.
(3)如图 1﹣1 中,过 D 作 GD⊥M1N1 交 M2N2 于 H,连接 OG、OH,作线段OG 的垂直平分线交 OC 于 F,作线段 OH 的垂直平分线交 BC 于点 F′.点 F 与点 F′即为所求.
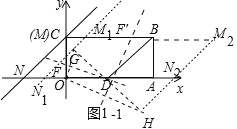
由题意可知 G(2﹣![]() ,
,![]() ),H(2+
),H(2+![]() ,﹣
,﹣![]() ),
),
线段 OG 的垂直平分线的解析式为 y=﹣(![]() ﹣1)x+2
﹣1)x+2 ![]() ﹣2,可得 F(0,2
﹣2,可得 F(0,2![]() ﹣2),
﹣2),
线段 OH 的垂直平分线的解析式为 y=(![]() +1)x﹣2
+1)x﹣2![]() ﹣2,可得 F′(2
﹣2,可得 F′(2![]() ,2).
,2).


科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与双曲线
与双曲线![]()
![]() 交于A点,且点A的横坐标是4.双曲线
交于A点,且点A的横坐标是4.双曲线![]()
![]() 上有一动点C(m,n),
上有一动点C(m,n), ![]() .过点A作
.过点A作![]() 轴垂线,垂足为B,过点C作
轴垂线,垂足为B,过点C作![]() 轴垂线,垂足为D,联结OC.
轴垂线,垂足为D,联结OC.

(1)求![]() 的值;
的值;
(2)设![]() 的重合部分的面积为S,求S与m的函数关系;
的重合部分的面积为S,求S与m的函数关系;
(3)联结AC,当第(2)问中S的值为1时,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
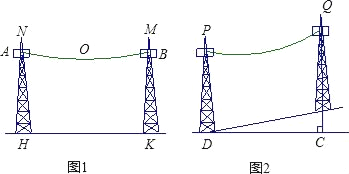
【题目】某种电缆在空中架设时,两端挂起的电缆下垂都近似成抛物线![]() 的形状,现按操作要求,电缆最低点离水平地面不得小于6米.
的形状,现按操作要求,电缆最低点离水平地面不得小于6米.
(1)如图1,若水平距离间隔80米建造一个电缆塔柱,求此电缆塔柱用于固定电缆的位置离地面至少应有多少米的高度?
(2)如图2,若在一个坡度为1:5的斜坡上,按水平距离间隔50米架设两固定电缆的位置离地面高度为20米的塔柱.
①求这种情况下在竖直方向上,下垂的电缆与斜坡的最近距离为多少米?
②这种情况下,直接写出下垂的电缆与地面的最近距离为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
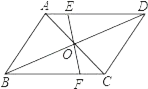
【题目】如图,平行四边形ABCD的对角线AC,BD交于O,EF过点O与AD,BC分别交于E,F,若AB=4,BC=5,OE=1.5,则四边形EFCD的周长_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
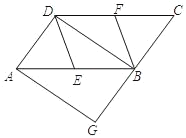
【题目】已知:如图,在ABCD中,AD=4,AB=8,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于点G.
(1)求证:△ADE≌△CBF;
(2)若四边形BEDF是菱形,求四边形AGBD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司投资销售一种进价为每件15元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:![]() ,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
(1)设该公司每月获得利润为w(元),求每月获得利润w(元)与销售单价x(元)之间的函数关系式,并确定自变量x的取值范围.
(2)当销售单价定为多少元时,每月可获得最大利润?每月的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC+∠EAD=180°,△ABC不动,△ADE绕点A旋转,连接BE,CD,F为BE的中点,连接AF.
(1)如图①,当∠BAE=90°时,求证:CD=2AF;
(2)当∠BAE≠90°时,(1)的结论是否成立?请结合图②说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“爱满扬州”慈善一日捐活动中,学校团总支为了了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成统计图.

(1)这50名同学捐款的众数为 元,中位数为 元;
(2)求这50名同学捐款的平均数;
(3)该校共有600名学生参与捐款,请估计该校学生的捐款总数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校奖励给王伟和李丽上海世博园门票共两张,其中一张为指定日门票,另一张为普通日门票。王伟和李丽分别转动下图的甲、乙两个转盘(转盘甲被二等分、转盘乙被三等分)确定指定日门票的归属,在两个转盘都停止转动后,若指针所指的两个数字之和为 偶数,则王伟获得指定日门票;若指针所指的两个数字之和为奇数,则李丽获得指定日门票;若指针指向分隔线,则重新转动。你认为这个方法公平吗?请画树状图或列表,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com