
����Ŀ��ij�ֵ����ڿ��м���ʱ�����˹���ĵ����´������Ƴ�������![]() ����״���ְ�����Ҫ������͵���ˮƽ���治��С��6�ף�
����״���ְ�����Ҫ������͵���ˮƽ���治��С��6�ף�
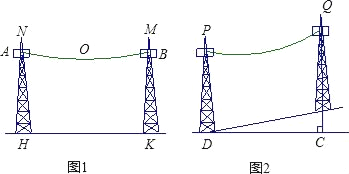
(1)��ͼ1����ˮƽ������80����һ��������������˵����������ڹ̶����µ�λ�����������Ӧ�ж����ĸ߶ȣ�
(2)��ͼ2������һ���¶�Ϊ1��5��б���ϣ���ˮƽ������50�������̶����µ�λ�������߶�Ϊ20��������
�����������������ֱ�����ϣ��´��ĵ�����б�µ��������Ϊ�����ף�
����������£�ֱ��д���´��ĵ����������������Ϊ�����ף�
���𰸡�(1) 22�ף�(2)��13.48�ף���17.75�ף�
��������
(1)��Ϊˮƽ������80�ף�˵����͵�ĺ�����Ϊ40������y=![]() ������߶ȣ�����6���ɣ�
������߶ȣ�����6���ɣ�
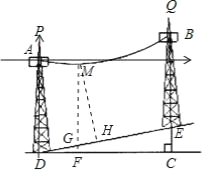
��2���Ե�DΪԭ����DC����Ϊx��������������ϵ���������ߵĽ���ʽΪy=![]() x2+bx+c����A��0��20����B(50��30)���룬����������ߵĽ���ʽ������D(0��0)��E(50��10)���ֱ��DE�Ľ���ʽ����һ����x�ᴹֱ��ֱ��x=m�������߽���M����б�½���G�������ʾMG����Ľ���ʽ����Сֵ������MH��DE��H��������MGH����DEC�Լ��¶�1��5����������´��ĵ�����б�µ��������MH�ij������������߽���ʽ����ֵ��������´������������������.
x2+bx+c����A��0��20����B(50��30)���룬����������ߵĽ���ʽ������D(0��0)��E(50��10)���ֱ��DE�Ľ���ʽ����һ����x�ᴹֱ��ֱ��x=m�������߽���M����б�½���G�������ʾMG����Ľ���ʽ����Сֵ������MH��DE��H��������MGH����DEC�Լ��¶�1��5����������´��ĵ�����б�µ��������MH�ij������������߽���ʽ����ֵ��������´������������������.
(1)y=![]() ��402=16��
��402=16��
16+6=22�ף�
�̶����µ�λ�����������Ӧ��22�ĸ߶ȣ�
(2)��ͼ������DΪ����ԭ�㣬DC����Ϊx����������ֱ������ϵ��
���ʱ�����߽���ʽΪy=![]() x2+bx+c��
x2+bx+c��
��֪��A��0��20����B��50��30�����������ʽ�����b=-![]() ��c��20��
��c��20��
��y=![]() x2��
x2��![]() x+20��
x+20��
�����б������ֱ�ߵĽ���ʽΪ��y=![]() x��
x��
��һ����x�ᴹֱ��ֱ��x=m�������߽���M����б�½���G��
��MG=![]() m2��
m2��![]() m+20��
m+20��![]() m��
m��![]() (m��25)2+13.75��
(m��25)2+13.75��
�൱m=25ʱ��MG����СֵΪ13.75����MH��DE��H��
MH=13.75��![]() ��5=13.48���ף���
��5=13.48���ף���
������ֱ�����ϣ��´��ĵ�����б�µ��������Ϊ13.48�ף�
�ڡ�y��![]() x2��
x2��![]() x+20��
x+20��![]() (x-15)2+17.75��
(x-15)2+17.75��
���´��ĵ����������������Ϊ17.75�ף�
�ʴ�Ϊ��(1) 22�ף�(2)��13.48�ף���17.75�ף�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��A(0��2)����AOBΪ�ȱ������Σ�P��x����һ������(����ԭ��O�غ�)�����߶�APΪһ�������Ҳ����ȱ�������APQ��
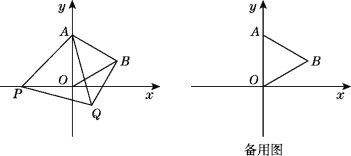
(1)���B�����꣮
(2)�ڵ�P�˶������У���ABQ�Ĵ�С�Ƿ����ı䣿�����ı䣬������С�����ı䣬��˵�����ɣ�
(3)����OQ����OQ��ABʱ�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���д��������![]() ����ˮ�����üס��ҡ������ַ�ʽ����װ����н������ۣ�ÿ�е��ܳɱ�Ϊ����
����ˮ�����üס��ҡ������ַ�ʽ����װ����н������ۣ�ÿ�е��ܳɱ�Ϊ����![]() ����ˮ���ɱ�֮�ͣ����ӳɱ����Բ��ƣ����ַ�ʽÿ�зֱ�װ
����ˮ���ɱ�֮�ͣ����ӳɱ����Բ��ƣ����ַ�ʽÿ�зֱ�װ![]() ����ˮ��
����ˮ��![]() �����ַ�ʽÿ�зֱ�װ
�����ַ�ʽÿ�зֱ�װ![]() ����ˮ��
����ˮ��![]() ����ÿ�е��ܳɱ���ÿǧ��
����ÿ�е��ܳɱ���ÿǧ��![]() ˮ���ɱ���
ˮ���ɱ���![]() ����ÿ�м�����������Ϊ
����ÿ�м�����������Ϊ![]() ��ÿ�мױ�ÿ���ҵ��ۼ۵�
��ÿ�мױ�ÿ���ҵ��ۼ۵�![]() ��ÿ�б��ڳɱ������
��ÿ�б��ڳɱ������![]() ��ۺ����۳��ۣ�����Ϊÿǧ��
��ۺ����۳��ۣ�����Ϊÿǧ��![]() ˮ���ɱ���
ˮ���ɱ���![]() ���������ۼס��ҡ������ַ�ʽ������������֮��Ϊ
���������ۼס��ҡ������ַ�ʽ������������֮��Ϊ![]() ʱ����������������Ϊ__________.
ʱ����������������Ϊ__________.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����С���ƻ����ڽ��μ�־Ը���С����μӾ��Ϸ�����С����μ����������������������ͨ������Ϸ�������μ��ĸ��������С�������һ����Ϸ����Ϸ�����ǣ���������ȫ��ͬ�Ŀ�Ƭ�Ϸֱ���4��5��6�������֣�һ���ȴ����ſ�Ƭ��������һ�ţ��������ֺ�Żأ���һ���ٴ���������һ�ţ��������֣�����������ſ�Ƭ��ǵ�����֮��Ϊż��������С�����뷨�μӾ��Ϸ���������������ſ�Ƭ��ǵ�����֮��Ϊ����������С�����뷨�μ��������������������Ϊ�����Ϸ��ƽ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�κ���y��kx+b��k��b�dz�����k��0����ͼ���A��1��3����B����1����1�����㣮
(1)���һ�κ����ı���ʽ��
(2)���㣨2a+2��a2���ڸ�һ�κ���ͼ���ϣ���a��ֵ��
(3)��֪��C��x1��y1���͵�D��x2��y2���ڸ�һ�κ���ͼ���ϣ���m����x1��x2����y1��y2�����жϷ���������y��![]() ��ͼ�����ڵ����ޣ�˵�����ɣ�
��ͼ�����ڵ����ޣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������ABCD����E��BA�ӳ����ϣ���F��BC�ϣ��ҡ�CDE��2��ADF��
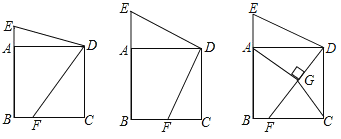
��1����֤����E��2��CDF��
��2����F��BC�е㣬��֤��AE+DE��2AD��
��3����AG��DF�ڵ�G����CG����CGȡ��Сֵʱ��ֱ��д��AE��AB��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���� OABC��O Ϊ����ԭ�㣬��֪ A��4��0����C��0��2����D Ϊ�� OA ���е㣬���� BD��M ���� C ���غϣ�N Ϊ x ����һ�㣬MN��BD�� ֱ�� MN ���� x ������ƽ�ƣ�
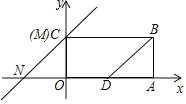
(1)���ı��� MBDN Ϊ����ʱ��N ��������� ��
(2)�� MN ƽ�Ƶ��δ�ʱ��ǡ�ý��ı��� ODBC �����Ϊ 1��3 �������֣��������ʱֱ�� MN �Ľ���ʽ��
(3)�ڣ�1���������£��ھ��� OABC ���������ϣ��Ƿ���ڵ� F������ DF�� ���������� DF ���ڵ�ֱ�߷��ۣ�ʹ�õ� O ǡ������ֱ�� MN �ϣ������ڣ� ��� F ������ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���![]() ��ͼ���뷴��������
��ͼ���뷴��������![]() ��ͼ���ڵڶ���������
��ͼ���ڵڶ���������![]() ��
��![]() ���㣬��
���㣬��![]() ��
��![]() ��ֱ���
��ֱ���![]() ��
��![]() ���㣬����
���㣬����![]() ��
��![]() ���ڵ�
���ڵ�![]() ������
������![]() ����
����![]() �����Ϊ3������
�����Ϊ3������![]() ����
����![]() ��ԳƵ�
��ԳƵ�![]() ��
��
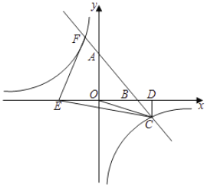
��1����һ�κ����ͷ����������Ľ���ʽ��
��2������![]() ��
��![]() ����
����![]() �������
�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com