
分析 (1)根据对称式的定义进行判断;
(2)①先得到a+b=-2,ab=$\frac{1}{2}$,再变形得到$\frac{b}{a}+\frac{a}{b}$=$\frac{{a}^{2}+{b}^{2}}{ab}$=$\frac{(a+b)^{2}-2ab}{ab}$,然后利用整体代入的方法计算;
②根据分式的性质变形得到$\frac{{{a^4}+1}}{a^2}+\frac{{{b^4}+1}}{b^2}$=a2+$\frac{1}{{a}^{2}}$+b2+$\frac{1}{{b}^{2}}$,再利用完全平方公式变形得到(a+b)2-2ab+$\frac{(a+b)^{2}-2ab}{{a}^{2}{b}^{2}}$,所以原式═$\frac{17}{16}$m2+$\frac{17}{2}$,然后根据非负数的性质可确定$\frac{{{a^4}+1}}{a^2}+\frac{{{b^4}+1}}{b^2}$的最小值.
解答 解:(1)式子①a2b2②a2-b2③$\frac{1}{a}+\frac{1}{b}$中,属于对称式的是 ①③.
故答案为①③;
(2)∵x2+(a+b)x+ab=x2+mx+n
∴a+b=m,ab=n.
①a+b=-2,ab=$\frac{1}{2}$,
$\frac{b}{a}+\frac{a}{b}$=$\frac{{a}^{2}+{b}^{2}}{ab}$=$\frac{(a+b)^{2}-2ab}{ab}$=$\frac{{2}^{2}-2×\frac{1}{2}}{\frac{1}{2}}$=6;
②$\frac{{{a^4}+1}}{a^2}+\frac{{{b^4}+1}}{b^2}$=a2+$\frac{1}{{a}^{2}}$+b2+$\frac{1}{{b}^{2}}$
=(a+b)2-2ab+$\frac{(a+b)^{2}-2ab}{{a}^{2}{b}^{2}}$
=m2+8+$\frac{{m}^{2}+8}{16}$
=$\frac{17}{16}$m2+$\frac{17}{2}$,
∵$\frac{17}{16}$m2≥0,
∴$\frac{{{a^4}+1}}{a^2}+\frac{{{b^4}+1}}{b^2}$的最小值为$\frac{17}{2}$.
点评 本题考查了分式的混合运算:分式的混合运算,要注意运算顺序,式与数有相同的混合运算顺序;先乘方,再乘除,然后加减,有括号的先算括号里面的;最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知反比例函数y=$\frac{2}{x}$的图象上有一组点B1,B2,…,Bn,它们的横坐标依次增加1,且点B1横坐标为1.“①,②,③…”分别表示如图所示的三角形的面积,记S1=①-②,S2=②-③,…,则S7的值为$\frac{1}{56}$,S1+S2+…+Sn=$\frac{n}{n+1}$(用含n的式子表示).
如图,已知反比例函数y=$\frac{2}{x}$的图象上有一组点B1,B2,…,Bn,它们的横坐标依次增加1,且点B1横坐标为1.“①,②,③…”分别表示如图所示的三角形的面积,记S1=①-②,S2=②-③,…,则S7的值为$\frac{1}{56}$,S1+S2+…+Sn=$\frac{n}{n+1}$(用含n的式子表示).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
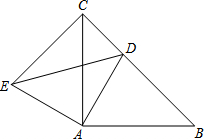 已知:如图,等腰△ABC,AB=AC,点D为△ABC的BC边上一点,连接AD,将线段AD旋转至AE,使得∠DAE=∠BAC,连接CE.
已知:如图,等腰△ABC,AB=AC,点D为△ABC的BC边上一点,连接AD,将线段AD旋转至AE,使得∠DAE=∠BAC,连接CE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 过直线l外一点P用直尺和圆规作直线l的垂线的方法是:以点P为圆心,大于点P到直线l的距离长为半径画弧,交直线l于点A、B;分别以A、B为圆心,大于$\frac{1}{2}$AB长为半径画弧,两弧交于点C.连结PC,则PC⊥AB.
过直线l外一点P用直尺和圆规作直线l的垂线的方法是:以点P为圆心,大于点P到直线l的距离长为半径画弧,交直线l于点A、B;分别以A、B为圆心,大于$\frac{1}{2}$AB长为半径画弧,两弧交于点C.连结PC,则PC⊥AB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com