

分析 (1)利用平行线的性质得出∠ADE=60°,再利用翻折变换的性质得出∠ADE=∠EDF=60°,进而得出∠BDF=60°即可得出答案;
(2)利用平行线的性质结合(1)中所求得出∠2,∠5+∠6的度数即可得出答案.
解答 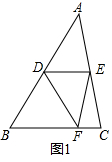 (1)证明:如图1,∵∠B=60°,DE∥BC,
(1)证明:如图1,∵∠B=60°,DE∥BC,
∴∠ADE=60°,
∵△ADE沿DE折叠,点A对应点为F点,
∴∠ADE=∠EDF=60°,
∴∠BDF=60°,
∴△BDF是等边三角形;
(2)解:如图2,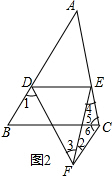 由(1)得:∠1=60°,
由(1)得:∠1=60°,
∵CF∥AB,
∴∠2+∠3=60°,∠B=∠6=60°,
∵∠B=60°,∠C=78°,
∴∠A=∠3=42°,
∴∠2=60°-42°=18°,
∴∠5+∠6=60°+78°=138°,
∴∠4=∠180°-18°-138°=24°.
点评 此题主要考查了翻折变换的性质以及平行线的性质和等边三角形的判定以及三角形内角和定理等知识,正确利用翻折变换的性质得出∠ADE=∠EDF是解题关键.


科目:初中数学 来源: 题型:选择题
 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,点D是AB上的一个动点,DE⊥AC于点E.DF⊥BC于点F,点D从点A出发向点B移动(不含A、B两点),若AD长为x,矩形DECF的周长为y,则下列图象能大致反映y与x的函数关系的是( )
如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,点D是AB上的一个动点,DE⊥AC于点E.DF⊥BC于点F,点D从点A出发向点B移动(不含A、B两点),若AD长为x,矩形DECF的周长为y,则下列图象能大致反映y与x的函数关系的是( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 25.30千克 | B. | 24.70千克 | C. | 25.51千克 | D. | 24.80千克 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 阅读下列材料:
阅读下列材料:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 问题提出:如图,已知:线段AB,试在平面内找到符合条件的所有点C,使∠ACB=30°.(利用直尺和圆规作图,保留作图痕迹,不写作法).
问题提出:如图,已知:线段AB,试在平面内找到符合条件的所有点C,使∠ACB=30°.(利用直尺和圆规作图,保留作图痕迹,不写作法).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-2,-3) | B. | (2,-3) | C. | (2,3) | D. | (-3,-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a0=1 | B. | (-3)-2=-$\frac{1}{9}$ | C. | $\sqrt{18}$-$\sqrt{32}$=-$\sqrt{2}$ | D. | $\sqrt{(-2)^{2}}$=-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 请在所给网格中按下列要求操作:
请在所给网格中按下列要求操作:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com