
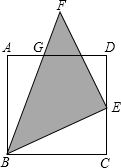
 如图,点E是正方形ABCD的CD边上的一点,以BE为一条直角边作等腰直角三角形BEF,斜边BF交AD于G,已知AG=5厘米,GD=15厘米.三角形BEF的面积是272厘米2.
如图,点E是正方形ABCD的CD边上的一点,以BE为一条直角边作等腰直角三角形BEF,斜边BF交AD于G,已知AG=5厘米,GD=15厘米.三角形BEF的面积是272厘米2. 分析 连接AC,交BF、BE于H、K,根据勾股定理求得AC=20$\sqrt{2}$,BG=5$\sqrt{17}$,根据AG∥BC,得出$\frac{AH}{HC}$=$\frac{GH}{HB}$=$\frac{1}{4}$,从而求得AH=4$\sqrt{2}$,HC=16$\sqrt{2}$,GH=$\sqrt{17}$,BH=4$\sqrt{17}$,证得△AHG∽△BHK,得出$\frac{AH}{BH}$=$\frac{GH}{HK}$,求得HK=$\frac{17}{2}$$\sqrt{2}$,得出AK=AH+HK=$\frac{25}{2}$$\sqrt{2}$,KC=AC-AK=$\frac{15}{2}$$\sqrt{2}$,根据AB∥CD,得出$\frac{CE}{AB}$=$\frac{CK}{AK}$,求得CE=12,然后根据勾股定理求得BE2=544,进而即可求得等腰直角三角形的面积.
解答 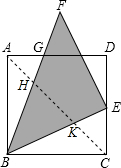 解:连接AC,交BF、BE于H、K,
解:连接AC,交BF、BE于H、K,
∵AG=5厘米,GD=15厘米,
∴AD=20厘米,
∴AB=BC=20厘米,
∴AC=20$\sqrt{2}$,BG=5$\sqrt{17}$,
∵AG∥BC,
∴$\frac{AH}{HC}$=$\frac{GH}{HB}$=$\frac{5}{20}$=$\frac{1}{4}$,
∴AH=4$\sqrt{2}$,HC=16$\sqrt{2}$,GH=$\sqrt{17}$,BH=4$\sqrt{17}$,
∵∠GAH=∠HBK=45°,∠AHG=∠BHK,
∴△AHG∽△BHK,
∴$\frac{AH}{BH}$=$\frac{GH}{HK}$,即$\frac{4\sqrt{2}}{4\sqrt{17}}$=$\frac{\sqrt{17}}{HK}$,
∴HK=$\frac{17}{2}$$\sqrt{2}$,
∴AK=AH+HK=4$\sqrt{2}$+$\frac{17}{2}$$\sqrt{2}$=$\frac{25}{2}$$\sqrt{2}$,
∴KC=AC-AK=20$\sqrt{2}$-$\frac{25}{2}$$\sqrt{2}$=$\frac{15}{2}$$\sqrt{2}$,
∵AB∥CD,
∴$\frac{CE}{AB}$=$\frac{CK}{AK}$,即$\frac{CE}{20}$=$\frac{\frac{15\sqrt{2}}{2}}{\frac{25\sqrt{2}}{2}}$,
∴CE=12,
∴BE2=BC2+CE2=544,
∴S△BEF=$\frac{1}{2}$BE2=$\frac{1}{2}$×544=272(厘米2),
故答案为272厘米2.
点评 本题考查了正方形的性质,三角形相似的判定和性质,勾股定理的应用,三角形的面积等,作出辅助线构建相似三角形是解题的关键.


 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com