
【题目】四边形ABCD内接于⊙O,连接AC、BD,2∠BDC+∠ADB=180°.
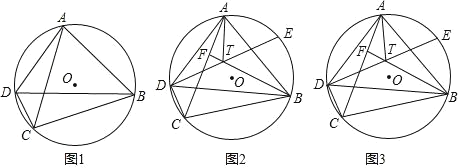
(1)如图1,求证:AC=BC;
(2)如图2,E为⊙O上一点,![]() =
=![]() ,F为AC上一点,DE与BF相交于点T,连接AT,若∠BFC=∠BDC+
,F为AC上一点,DE与BF相交于点T,连接AT,若∠BFC=∠BDC+![]() ∠ABD,求证:AT平分∠DAB;
∠ABD,求证:AT平分∠DAB;
(3)在(2)的条件下,DT=TE,AD=8,BD=12,求DE的长.
【答案】(1)见解析;(2)见解析;(3)8![]()
【解析】
(1)只要证明∠CAB=∠CBA即可.
(2)如图2中,作TH⊥AD于H,TR⊥BD于R,TL⊥AB于L.想办法证明TL=TH即可解决问题.
(3)如图3中,连接EA,EB,作EG⊥AB,TH⊥AD于H,TR⊥BD于R,TL⊥AB于L,AQ⊥BD于Q.证明△EAG≌△TDH(AAS),推出AG=DH,证明Rt△TDR≌Rt△TDH(HL),推出DH=DR,同理可得AL=AH,BR=BL,设DH=x,则AB=2x,
由S△ADB=![]() BDAQ=
BDAQ=![]() ADh+
ADh+![]() ABh+
ABh+![]() DBh,可得AQ=
DBh,可得AQ=![]() h,再根据sin∠BDE=sin∠ADE,sin∠AED=sin∠ABD,构建方程组求出m即可解决问题.
h,再根据sin∠BDE=sin∠ADE,sin∠AED=sin∠ABD,构建方程组求出m即可解决问题.
解:(1)如图1中,
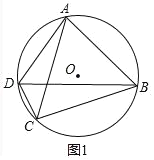
∵四边形ABCD内接于⊙O,
∴∠ADC+∠ABC=180°,
即∠ADB+∠BDC+∠ABC=180°,
∵2∠BDC+∠ADB=180°,
∴∠ABC=∠BDC,
∵∠BAC=∠BDC,
∴∠BAC=∠ABC,
∴AC=BC.
(2)如图2中,作TH⊥AD于H,TR⊥BD于R,TL⊥AB于L.
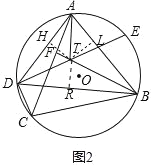
∵∠BFC=∠BAC+∠ABF,∠BAC=∠BDC,
∴∠BFC=∠BDC+∠ABF,
∵∠BFC=∠BDC+![]() ∠ABD,
∠ABD,
∴∠ABF=![]() ∠ABD,
∠ABD,
∴BT平分∠ABD,
∵![]() =
=![]()
∴∠ADE=∠BDE,
∴DT平分∠ADB,
∵TH⊥AD于H,TR⊥BD于R,TL⊥AB于L.
∴TR=TL,TR=TH,/p>
∴TL=TH,
∴AT平分∠DAB.
(3)如图3中,连接EA,EB,作EG⊥AB,TH⊥AD于H,TR⊥BD于R,TL⊥AB于L,AQ⊥BD于Q.
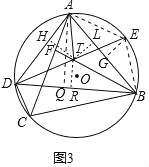
∵![]() =
=![]()
∴∠EAB=∠EDB=∠EDA,AE=BE,
∵∠TAE=∠EAB+∠TAB,∠ATE=∠EDA+∠DAT,
∴∠TAE=∠ATE,
∴AE=TE,
∵DT=TE,
∴AE=DT,
∵∠AGE=∠DHT=90°,
∴△EAG≌△TDH(AAS),
∴AG=DH,
∵AE=EB,EG⊥AB,
∴AG=BG,
∴2DH=AB,
∵Rt△TDR≌Rt△TDH(HL),
∴DH=DR,同理可得AL=AH,BR=BL,
设DH=x,则AB=2x,
∵AD=8,DB=12,
∴AL=AH=8﹣x,BR=12﹣x,AB=2x=8﹣x+12﹣x,
∴x=5,
∴DH=5,AB=10,
设TR=TL=TH=h,DT=m,
∵S△ADB=![]() BDAQ=
BDAQ=![]() ADh+
ADh+![]() ABh+
ABh+![]() DBh,
DBh,
∴12AQ=(8+12+10)h,
∴AQ=![]() h,
h,
∵sin∠BDE=sin∠ADE,可得![]() =
=![]() =
=![]() ,
,
sin∠AED=sin∠ABD,可得![]() =
=![]() =
=![]() =
=![]() ,
,
∴![]() =
=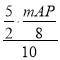 ,
,
解得m=4![]() 或﹣4
或﹣4![]() (舍弃),
(舍弃),
∴DE=2m=8![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
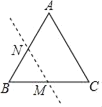
【题目】如图,在等边△ABC中,AB=4cm,点M为边BC的中点,点N为边AB上的任意一点(不与点A,B重合).若点B关于直线MN的对称点B'恰好落在等边△ABC的边上,则BN的长为_____cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,函数y=﹣x2+bx+c的部分图象与x轴、y轴的交点分别为A(1,0),B(0,3),对称轴是x=﹣1,在下列结论中,正确的是( )

A.顶点坐标为(﹣1,3)
B.抛物线与x轴的另一个交点是(﹣4,0)
C.当x<0时,y随x的增大而增大
D.b+c=1
查看答案和解析>>
科目:初中数学 来源: 题型:
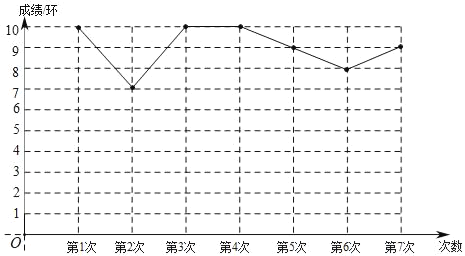
【题目】嘉淇同学利用业余时间进行射击训练,一共射击7次,经过统计,制成如图12所示的折线统计图.
(1)这组成绩的众数是 ;
(2)求这组成绩的方差;
(3)若嘉淇再射击一次(成绩为整数环),得到这8次射击成绩的中位数恰好就是原来7次成绩的中位数,求第8次的射击成绩的最大环数.
查看答案和解析>>
科目:初中数学 来源: 题型:
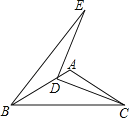
【题目】如图,在△ABC中,AB=AC,∠BAC=120°,点D为AB边上一点(不与点B重合),连接CD,将线段CD绕点D逆时针旋转90°,点C的对应点为E,连接BE.若AB=2,则△BDE面积的最大值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx﹣3(a≠0,且a,b为常数)的图象经过点(2,1)和(3,0).
(1)试求这条抛物线的解析式;
(2)若将抛物线进行上、下或左、右平移,请你写出一种平移的方法,使平移后的抛物线顶点落在直线y=x上,并直接写出平移后抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
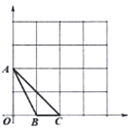
【题目】如图,在下列![]() (边长为1)的网格中,已知
(边长为1)的网格中,已知![]() 的三个顶点
的三个顶点![]() ,
,![]() ,
,![]() 在格点上,请分别按不同要求在网格中描出一个格点
在格点上,请分别按不同要求在网格中描出一个格点![]() ,并写出点
,并写出点![]() 的坐标.
的坐标.
(1)将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,画出旋转后所得的三角形,点
,画出旋转后所得的三角形,点![]() 旋转后落点为
旋转后落点为![]() .
.
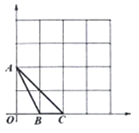
(2)经过![]() ,
,![]() ,
,![]() 三点有一条抛物线,请找到点
三点有一条抛物线,请找到点![]() ,使点
,使点![]() 也落在这条抛物线上.
也落在这条抛物线上.
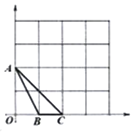
(3)经过![]() ,
,![]() ,
,![]() 三点有一个圆,请找到一个横坐标为2的点
三点有一个圆,请找到一个横坐标为2的点![]() ,使点
,使点![]() 也落在这个圆上.
也落在这个圆上.
(1)点![]() 的坐标为(
的坐标为(
(2)点![]() 的坐标为( , )
的坐标为( , )
(3)点![]() 的坐标为( , )
的坐标为( , )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com