
【题目】四边形ADBC中,AC=BC,∠ACB=90°, ∠ADB=30°,AD=![]() ,CD=14, 则BD=_________
,CD=14, 则BD=_________

【答案】![]()
【解析】
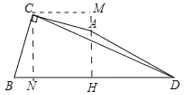
作AH⊥BD于H,CN⊥BD于N,CM⊥HA于M,则四边形CMHN是矩形.首先证明△BCN≌△ACM,得四边形CMHN是正方形,设CN=a.构建方程求出a即可解决问题;
解:作AH⊥BD于H,CN⊥BD于N,CM⊥HA于M,则四边形CMHN是矩形.
∵∠BCA=∠MCN=90°,
∴∠BCN=∠MCA,
∵∠CNB=∠M=90°,BC=CA,
∴△BCN≌△ACM,
∴CM=CN,BN=AM,
∴四边形CMHN是正方形,设CN=a.
在Rt△AHD中,AD=![]() ,∠ADH=30°,
,∠ADH=30°,
∴AH=![]() ,DH=
,DH=![]() ,
,
在Rt△CND中,∵CN2+DN2=CD2,
∴a2+(a+![]() )2=142,
)2=142,
解得a=![]() 或
或![]() (舍去),
(舍去),
∴AM=BN=![]() ,
,
∴BD=BN+NH+DH=![]() ,
,
故答案为:![]() .
.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
【题目】湘潭市继2017年成功创建全国文明城市之后,又准备争创全国卫生城市.某小区积极响应,决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买2个温馨提示牌和3个垃圾箱共需550元,且垃圾箱的单价是温馨提示牌单价的3倍.
(1)求温馨提示牌和垃圾箱的单价各是多少元?
(2)该小区至少需要安放48个垃圾箱,如果购买温馨提示牌和垃圾箱共100个,且费用不超过10000元,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,Rt△ABM和Rt△ADN的斜边分别为正方形的边AB和AD,其中AM=AN,线段MN与线段AD相交于点T,若AD=3AT,则tan∠ABM= ;

(2)如图2,在菱形ABCD中,CD=6,∠ADC=60°,菱形形内部有一动点P,满足S△PAB=![]() S菱形ABCD,则点P到A、B两点的距离之和PA+PB的最小值为 .
S菱形ABCD,则点P到A、B两点的距离之和PA+PB的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD内接于⊙O,连接AC、BD,2∠BDC+∠ADB=180°.
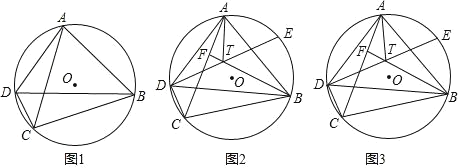
(1)如图1,求证:AC=BC;
(2)如图2,E为⊙O上一点,![]() =
=![]() ,F为AC上一点,DE与BF相交于点T,连接AT,若∠BFC=∠BDC+
,F为AC上一点,DE与BF相交于点T,连接AT,若∠BFC=∠BDC+![]() ∠ABD,求证:AT平分∠DAB;
∠ABD,求证:AT平分∠DAB;
(3)在(2)的条件下,DT=TE,AD=8,BD=12,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AC=BC,∠ACB=90°,直线l经过直角顶点C,AD⊥l,BE⊥l,垂足分别为D、E.

(1)如图,若AD=1,BE=3,求DE的长度.
(2)当直线l绕C点转动时,若AD=a,BE=b.请画出示意的图形并用含a、b的代数式直接表示出DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD,DEFG都是正方形,边长分别为m,n(m<n).坐标原点O为AD的中点,A,D,E在y轴上,若二次函数y=ax2的图象过C,F两点,则![]() =( )
=( )

A.![]() +1B.
+1B.![]() +1C.2
+1C.2![]() ﹣1D.2
﹣1D.2![]() ﹣1
﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:r如图,在梯形ABCD中,AD∥BC,∠BCD=90°.对角线AC、BD相交于点E。且AC⊥BD。(1)求证:CD=BC·AD;(2)点F是边BC上一点,连接AF,与BD相交于点G,如果∠BAF=∠DBF,求证:![]() 。
。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰![]() 中,
中,![]() ,AD是
,AD是![]() 的角平分线,且
的角平分线,且![]() ,以点A为圆心,AD长为半径画弧EF,交AB于点E,交AC于点F.
,以点A为圆心,AD长为半径画弧EF,交AB于点E,交AC于点F.

(1)求由弧EF及线段FC、CB、BE围成图形(图中阴影部分)的面积;
(2)将阴影部分剪掉,余下扇形AEF,将扇形AEF围成一个圆锥的侧面,AE与AF正好重合,圆锥侧面无重叠,求这个圆锥的高h.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com