【题目】有一根长
的金属棒，欲将其截成
根
长的小段和
根
长的小段，剩余部分作废料处理，若使废料最少，则正整数
应分别为（ ）
【答案】B
【解析】根据题意得：7x+9y≤40，
则
∵40-9y≥0且y是非负整数，
∴y的值可以是：0或1或2或3或4．
当x的值最大时，废料最少，
因而当y=0时，x≤40/7 ，则x=5，此时，所剩的废料是：40-5×7=5mm；
当y=1时，x≤31/7 ，则x=4，此时，所剩的废料是：40-1×9-4×7=3mm；
当y=2时，x≤22/7 ，则x=3，此时，所剩的废料是：40-2×9-3×7=1mm；
当y=3时，x≤13/7 ，则x=1，此时，所剩的废料是：40-3×9-7=6mm；
当y=4时，x≤4/7 ，则x=0，此时，所剩的废料是：40-4×9=4mm．
则最小的是：x=3，y=2．
故选B．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AD是BC边上的高，AE是∠BAC的平分线，若∠B＝56°，∠C＝42°，则∠DAE的度数为（ ）
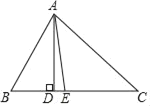
A. 3°B. 7°C. 11°D. 15°
查看答案和解析>>
科目：初中数学 来源： 题型：
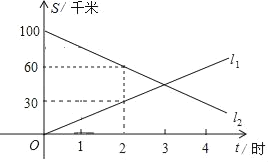
【题目】A，B两地相距100千米，甲，乙两人骑车同时分别从A、B两地相向而行，假设他们都保持匀速行驶，直线l1，l2分别表示甲，乙两人与A地的距离S（单位：km）与行驶时间t（单位：h）之间关系的图象．
根据图象提供的信息，解答下列问题：
（1）甲、乙两人的速度分别是多少？
（2）经过多长时间，两人相遇？
（3）分别写出甲，乙两人与A地的距离S（单位：km）与行驶时间t（单位：h）之间的关系式．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（6分）如图，在△OAB中，∠OAB=90°，OA=AB=6，将△OAB绕点O逆时针方向旋转90°得到△OA1B1．
（1）线段A1B1的长是 ；∠AOB1的度数是 ．
（2）连接AA1，求证：四边形OAA1B1是平行四边形．
查看答案和解析>>
科目：初中数学 来源： 题型：
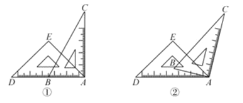
【题目】一副直角三角尺如图①叠放，现将45°的三角尺ADE固定不动，将含30°的三角尺ABC绕顶点A顺时针转动，要求两块三角尺的一组边互相平行.如图②，当∠BAD=15°时，有一组边BC∥DE，请再写出两个符合要求的∠BAD（0°＜∠BAD＜180°）的度数_________.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，四边形ABCD为矩形，O为AC中点，过点O作AC的垂线分别交AD、BC于点E、F，连接AF、CE．
（1）求证：四边形AFCE是菱形；
（2）若AC=8，EF=6，求BF的长.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】问题提出
如图①，
、
是⊙
的两条弦， 
， 
是
的中点， 
，垂足为
．
求证： 
．
小敏在解答此题时，利用了“补短法”进行证明，她的方法如下：
如图②，延长
至
，使
，连接
、
、
、
、
．
（请你在下面的空白处完成小敏的证明过程．）
推广运用
如图③，等边
内接于⊙
， 
． 
是
上一点， 
， 
，垂足为
，则
的周长是__________．
拓展研究
如图④，若将“问题提出”中的“
是
的中点”改成“
是
的中点”，其余条件不变，“
”这一结论还成立吗？若成立，请说明理由；若不成立，写出
、
、
三者之间存在的关系并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，有一个可以自由转动的转盘被平均分成3个扇形，分别标有1，2，3三个数字．小王和小李各转动一次转盘为一次游戏，当每次转盘停止后，指针所指扇形内的数为各自所得的数，一次游戏结束后得到一组数（若指针指在分界线时重转）．
（1）请你用树状图或列表的方法表示出每次游戏可能出现的所有结果；
（2）求每次游戏后得到的一组数恰好是方程x2﹣4x+3=0的解的概率．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
