
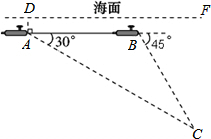
 如图,一艘核潜艇在海面DF下615米A点处测得俯角为30°正前方的海底C点处有黑匣子,继续在同一深度直线航行1 025米到B点处测得正前方C点处的俯角为45°.求海底C点处距离海面DF的深度(结果精确到个位,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732).
如图,一艘核潜艇在海面DF下615米A点处测得俯角为30°正前方的海底C点处有黑匣子,继续在同一深度直线航行1 025米到B点处测得正前方C点处的俯角为45°.求海底C点处距离海面DF的深度(结果精确到个位,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732). 分析 首先作CE⊥AB于E,依题意,AB=1025,∠EAC=30°,∠CBE=45°,设CE=x,则BE=x,进而利用正切函数的定义求出x即可.
解答 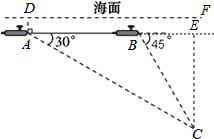 解:作CE⊥AB于E,
解:作CE⊥AB于E,
依题意,AB=1025,∠EAC=30°,∠CBE=45°,
设CE=x,则BE=x,
Rt△ACE中,tan30°=$\frac{CE}{AE}$=$\frac{x}{1025+x}$=$\frac{\sqrt{3}}{3}$,
整理得出:3x=1025$\sqrt{3}$+$\sqrt{3}$x,
解得:x=$\frac{1025}{2}$($\sqrt{3}$+1)≈1400.15米,
则海底C点处距离海面DF的深度=x+615≈2015米.
答:海底C点处距离海面DF的深度约为2015米.
点评 此题主要考查了俯角的定义及其解直角三角形的应用,解题时首先正确理解俯角的定义,然后利用三角函数和已知条件构造方程解决问题.


科目:初中数学 来源: 题型:填空题
 如图所示,在?ABCD中,AE⊥BC于E,AF⊥CD于F,∠BAD=120°,BE=2,FD=3,则∠EAF=60°,?ABCD的周长为20.
如图所示,在?ABCD中,AE⊥BC于E,AF⊥CD于F,∠BAD=120°,BE=2,FD=3,则∠EAF=60°,?ABCD的周长为20.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3.61×106km2 | B. | 3.61×107km2 | C. | 0.361×108km2 | D. | 3.61×109km2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 16 | B. | ±4 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 35×103 | B. | 3.5×104 | C. | 0.35×105 | D. | 3.5×103 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com