
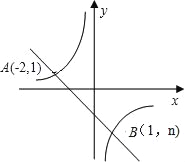
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于A、B两点.
的图象交于A、B两点.
(1)利用图中条件,求反比例函数的解析式及n的值.
(2)求一次函数的解析式.
(3)根据图象写出使一次函数的值大于反比例函数值的x的取值范围.
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案科目:初中数学 来源: 题型:
【题目】将两块斜边长相等的等腰直角三角板按如图①摆放,斜边AB分别交CD,CE于M,N点.
(1)如果把图①中的△BCN绕点C逆时针旋转90°得到△ACF,连接FM,如图②,求证:△CMF≌△CMN;
(2)将△CED绕点C旋转,则:
①当点M,N在AB上(不与点A,B重合)时,线段AM,MN,NB之间有一个不变的关系式,请你写出这个关系式,并说明理由;
②当点M在AB上,点N在AB的延长线上(如图③)时,①中的关系式是否仍然成立?

查看答案和解析>>
科目:初中数学 来源: 题型:
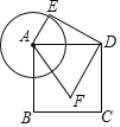
【题目】如图,已知正方形ABCD的边长为3,以点A为圆心,1为半径作圆,E是⊙A上的任意一点,将DE绕点D按逆时针旋转90°,得到DF,连接AF,
(1)当∠EAD=90°时,AF=________________.
(2)在E的整个运动过程中,AF的最大值是________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=ax+b(a≠0)的图象与反比例函数y2=![]() (k为常数,k≠0)的图象交于A、B两点,过点A作AC⊥x轴,垂足为C,连接OA,已知OC=2,tan∠AOC=
(k为常数,k≠0)的图象交于A、B两点,过点A作AC⊥x轴,垂足为C,连接OA,已知OC=2,tan∠AOC=![]() ,B(m,﹣2)
,B(m,﹣2)
(1)求一次函数和反比例函数的解析式.
(2)结合图象直接写出:当y1>y2时,x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
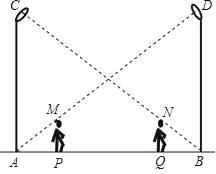
【题目】如图,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行20m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部,已知丁轩同学的身高是1.5m,两个路灯的高度都是9m,则两路灯之间的距离是_____m.
查看答案和解析>>
科目:初中数学 来源: 题型:
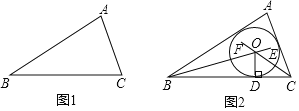
【题目】阅读下面材料:
在数学课上,老师提出利用尺规作图完成下面问题:
已知:![]() 求作:
求作:![]() 的内切圆.
的内切圆.
小明的作法如下:如图2,
![]() 作
作![]() ,
,![]() 的平分线BE和CF,两线相交于点O;
的平分线BE和CF,两线相交于点O;
![]() 过点O作
过点O作![]() ,垂足为点D;
,垂足为点D;
![]() 点O为圆心,OD长为半径作
点O为圆心,OD长为半径作![]() 所以,
所以,![]() 即为所求作的圆.
即为所求作的圆.
请回答:该尺规作图的依据是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,跳台滑雪是冬季奥运会比赛项目之一,运动员起跳后的飞行路线可以看作是抛物线的一部分,运动员起跳后的竖直高度y(单位:m)与水平距离x(单位:m)近似满足函数关系y=ax2+bx+c(a≠0).如图记录了某运动员起跳后的x与y的三组数据,根据上述函数模型和数据,可推断出该运动员起跳后飞行到最高点时,水平距离为( )
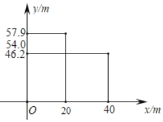
A. 10mB. 20mC. 15mD. 22.5m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com