

���� ��1����ͼ1����AD��BGΪ�����ߣ�����ͬ�ǵ������ȵõ�һ�Խ���ȣ�����һ��ֱ����ȣ�AG=BG������ASA�õ�������AHG��������BCGȫ�ȣ�����ȫ�������εĶ�Ӧ����ȵõ�AH=BC����AB=AC����AD��ֱ��BC���������ߺ�һ�õ�DΪBC�е㣬��BC=2BD�������������ɵ�֤��
��2��������BAC��Ϊ�۽ǣ������������䣬�����Ľ��ۻ�����������Ϊ����ͼ2����AD��BGΪ�����ߣ�����ͬ�ǵ������ȵõ�һ�Խ���ȣ�����һ��ֱ����ȣ�AG=BG������ASA�õ�������AHG��������BCGȫ�ȣ�����ȫ�������εĶ�Ӧ����ȵõ�AH=BC����AB=AC����AD��ֱ��BC���������ߺ�һ�õ�DΪBC�е㣬��BC=2BD�������������ɵ�֤��
��� 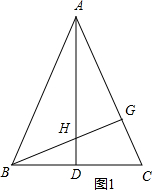 ��1��֤������ͼ1��
��1��֤������ͼ1��
��AD��BC��BG��AC��
���CAD+��C=90�㣬��CBG+��C=90�㣬
���CAD=��CBG������GAH=��CBG��
�ڡ�AHG�͡�BCG�У�
$\left\{\begin{array}{l}{��GAH=��CBG}\\{AG=BG}\\{��AGH=��BGC=90��}\end{array}\right.$��
���AHG�ա�BCG��ASA����
��AH=BC��
��AB=AC��AD��BC��
��BD=CD=$\frac{1}{2}$BC����BC=2BD��
��AH=2BD��
�ʴ�Ϊ��AH=BC��AHƽ��BC��
��2���⣺������BAC��Ϊ�۽ǣ������������䣬�����Ľ�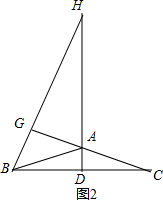 �ۻ�������
�ۻ�������
֤������ͼ2����AD��BC��BG��AG��
���CAD+��C=90�㣬��CBG+��C=90�㣬
���CAD=��CBG������GAH=��CBG��
�ڡ�AHG�͡�BCG�У�
$\left\{\begin{array}{l}{��GAH=��CBG}\\{AG=BG}\\{��AGH=��BGC=90��}\end{array}\right.$��
���AHG�ա�BCG��ASA����
��AH=BC��
��AB=AC��AD��BC��
��BD=CD=$\frac{1}{2}$BC����BC=2BD��
��AH=2BD��
���� ���⿼����ȫ�������ε��ж������ʣ���������ȫ�������ε��ж��������ǽⱾ��Ĺؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
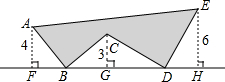 ��ͼ��AB=BC��CD=DE��AB��BC��CD��DE��AF��FH��CG��FH��EH��FH��AF=4��CG=3��EH=6����Ӱ�������Ϊ50��
��ͼ��AB=BC��CD=DE��AB��BC��CD��DE��AF��FH��CG��FH��EH��FH��AF=4��CG=3��EH=6����Ӱ�������Ϊ50���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
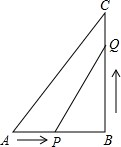 ��֪����ͼ��Rt��ABC�У���B=90�㣬AB=6cm��BC=8cm����P�ɵ�A������AB�������յ��B�����ƶ����ٶ�Ϊ1cm/s����Q�ɵ�B������BC�������յ��C�����ƶ����ٶ�Ϊ2cm/s���������P��Qͬʱ��A��B��������P��Q�����յ�ʱ�˶�ֹͣ���������Q��B��PΪ��������������ABC���ƣ�
��֪����ͼ��Rt��ABC�У���B=90�㣬AB=6cm��BC=8cm����P�ɵ�A������AB�������յ��B�����ƶ����ٶ�Ϊ1cm/s����Q�ɵ�B������BC�������յ��C�����ƶ����ٶ�Ϊ2cm/s���������P��Qͬʱ��A��B��������P��Q�����յ�ʱ�˶�ֹͣ���������Q��B��PΪ��������������ABC���ƣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2��4��3 | B�� | 3��4��-5 | C�� | 3��4��5 | D�� | 2��4��-5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ACB���ECD���ǵ���ֱ�������Σ���ACB=��ECD=90�㣬��DΪAB���ϵ�һ�㣬
��ͼ����ACB���ECD���ǵ���ֱ�������Σ���ACB=��ECD=90�㣬��DΪAB���ϵ�һ�㣬�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
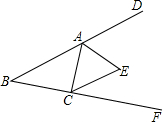 ��ͼ���ڡ�ABC�У���B=40�㣬�����ε���ǡ�DAC�͡�ACF��ƽ���߽��ڵ�E�����AEC�Ķ���Ϊ��������
��ͼ���ڡ�ABC�У���B=40�㣬�����ε���ǡ�DAC�͡�ACF��ƽ���߽��ڵ�E�����AEC�Ķ���Ϊ��������| A�� | 40�� | B�� | 50�� | C�� | 60�� | D�� | 70�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com