
分析 首先根据题意画出树状图,然后由树状图求得所有等可能的结果,即可求得求概率,比较大小,即可知这个游戏是否公平.
解答 解:画树状图得: ,
,
由图可得共有9种等可能的结果为:2,3,4,3,4,5,4,5,6;
∵两次摸出的球的标号之和为偶数的有5种情况,两次摸出的球的标号之和为奇数的有4种情况,
∴P(甲胜)=$\frac{5}{9}$,P(乙胜)=$\frac{4}{9}$.
∴P(甲胜)≠P(乙胜),
故这个游戏不公平,
可改规则为两次摸出的球的标号之和大于4甲胜,两次摸出的球的标号之和小于4乙胜.
点评 本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
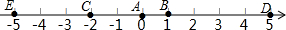 如图,A点的初始位置位于数轴上的原点,现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样至少移动1001次后该点到原点的距离不小于1499.
如图,A点的初始位置位于数轴上的原点,现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样至少移动1001次后该点到原点的距离不小于1499.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,数轴上有A、B、C、O四点,点O是原点,BC=$\frac{1}{3}$AB=8,OB比AO的$\frac{1}{4}$少1.
如图,数轴上有A、B、C、O四点,点O是原点,BC=$\frac{1}{3}$AB=8,OB比AO的$\frac{1}{4}$少1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
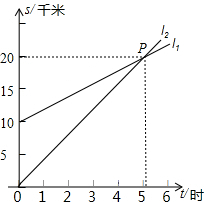 如图,l1反映了甲离开A地的时间与离A地的距离的关系l2反映了乙离开A地的时间与离开A地距离之间的关系,根据图象填空:
如图,l1反映了甲离开A地的时间与离A地的距离的关系l2反映了乙离开A地的时间与离开A地距离之间的关系,根据图象填空:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com