
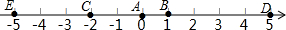 如图,A点的初始位置位于数轴上的原点,现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样至少移动1001次后该点到原点的距离不小于1499.
如图,A点的初始位置位于数轴上的原点,现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样至少移动1001次后该点到原点的距离不小于1499. 分析 利用题意得到移动1次后到原点的距离为1;移动2次后到原点的距离为2;移动3次后到原点的距离为4;移动4次后到原点的距离为5;移动5次后该点到原点的距离为7;移动6次后该点到原点的距离为8,于是可得移动(2n-1)次后该点到原点的距离为3n-2;移动2n次后该点到原点的距离为3n-1;当3n-2≥1499时,得到n最小值为501,当3n-1≥1499时,得到n最小值为500,所以至少移动1001次后该点到原点的距离不小于1499.
解答 解:由题意可得:
移动1次后该点对应的数为0+1=1,到原点的距离为1;
移动2次后该点对应的数为1-3=-2,到原点的距离为2;
移动3次后该点对应的数为-2+6=4,到原点的距离为4;
移动4次后该点对应的数为4-9=-5,到原点的距离为5;
移动5次后该点对应的数为-5+12=7,到原点的距离为7;
移动6次后该点对应的数为7-15=-8,到原点的距离为8;
…
故移动(2n-1)次后该点到原点的距离为3n-2;
移动2n次后该点到原点的距离为3n-1.
①当3n-2≥1499时,
解得:n≥500$\frac{1}{3}$,
∵n是正整数,
∴n最小值为501,此时移动了501次.
②当3n-1≥1499时,
解得:n≥500
∵n是正整数,
∴n最小值为500,此时移动了500次.
所以至少移动1001次后该点到原点的距离不小于1499.
点评 本题考查了数轴:规定了原点、正方向、单位长度的直线叫做数轴.解决本题的关键是得到移动(2n-1)次后该点到原点的距离为3n-2;移动2n次后该点到原点的距离为3n-1.


科目:初中数学 来源: 题型:解答题
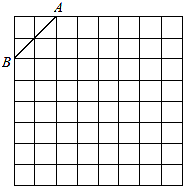 如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | … | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 3 | 0 | -1 | 0 | 3 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
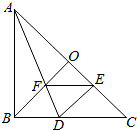 如图,在Rt△ABC中,AB=CB,BO⊥AC,把△ABC折叠,使AB落在AC上,点B与AC上的点E重合,展开后,折痕AD交BO于点F,连接DE、EF,下列结论:①AB=2BD;②图中有4对全等三角形;③若将△DEF沿EF折叠,则点O不一定落在AC上;④BD=BF,上述结论中正确的是( )
如图,在Rt△ABC中,AB=CB,BO⊥AC,把△ABC折叠,使AB落在AC上,点B与AC上的点E重合,展开后,折痕AD交BO于点F,连接DE、EF,下列结论:①AB=2BD;②图中有4对全等三角形;③若将△DEF沿EF折叠,则点O不一定落在AC上;④BD=BF,上述结论中正确的是( )| A. | ①②③④ | B. | ②④ | C. | ①③④ | D. | ①②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
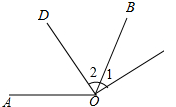 (1)已知一个角是它的余角的一半,求这个角的度数;
(1)已知一个角是它的余角的一半,求这个角的度数;查看答案和解析>>
科目:初中数学 来源: 题型:填空题
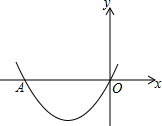 如图,在直角坐标系xOy中,若抛物线y=$\frac{1}{2}{x^2}$+2x交x轴的负半轴于A,以O为旋转中心,将线段OA按逆时针方向旋转α(0°<α≤360°),再沿水平方向向右或向左平移若干个单位长度,对应线段的一个端点正好落在抛物线的顶点处,请直接写出所有符合题意的α的值是30°或150°.
如图,在直角坐标系xOy中,若抛物线y=$\frac{1}{2}{x^2}$+2x交x轴的负半轴于A,以O为旋转中心,将线段OA按逆时针方向旋转α(0°<α≤360°),再沿水平方向向右或向左平移若干个单位长度,对应线段的一个端点正好落在抛物线的顶点处,请直接写出所有符合题意的α的值是30°或150°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com