
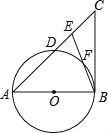
【题目】如图,在△ABC中,E是AC边上的一点,且AE=AB,∠BAC=2∠CBE,以AB为直径作⊙O交AC于点D,交BE于点F.
(1)求证:BC是⊙O的切线;
(2)若AB=8,BC=6,求DE的长.
【答案】(1)证明见解析(2)1.6
【解析】
试题分析:(1)由AE=AB,可得∠ABE=90°﹣![]() ∠BAC,又由∠BAC=2∠CBE,可求得∠ABC=∠ABE+∠CBE=90°,继而证得结论;
∠BAC,又由∠BAC=2∠CBE,可求得∠ABC=∠ABE+∠CBE=90°,继而证得结论;
(2)首先连接BD,易证得△ABD∽△ACB,然后由相似三角形的对应边成比例,求得答案.
试题解析:(1)∵AE=AB,
∴△ABE是等腰三角形,
∴∠ABE=![]() (180°﹣∠BAC=)=90°﹣
(180°﹣∠BAC=)=90°﹣![]() ∠BAC,
∠BAC,
∵∠BAC=2∠CBE,
∴∠CBE=![]() ∠BAC,
∠BAC,
∴∠ABC=∠ABE+∠CBE=(90°﹣![]() ∠BAC)+
∠BAC)+![]() ∠BAC=90°,
∠BAC=90°,
即AB⊥BC,
∴BC是⊙O的切线;
(2)连接BD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠ABC=90°,
∴∠ADB=∠ABC,
∵∠A=∠A,
∴△ABD∽△ACB,
∴![]() ,
,
∵在Rt△ABC中,AB=8,BC=6,
∴AC=![]() =10,
=10,
∴![]() ,
,
解得:AD=6.4,
∵AE=AB=8,
∴DE=AE﹣AD=8﹣6.4=1.6.


科目:初中数学 来源: 题型:
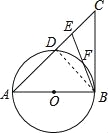
【题目】如图,已知以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为弧BE的中点,连接AD交OE于点F,若AC=FC
(Ⅰ)求证:AC是⊙O的切线;
(Ⅱ)若BF=5,DF=![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:如图,线段AC上依次有D,B,E三点,其中点B为线段AC的中点,AD=BE,若DE=4,求线段AC的长. ![]()
请补全以下解答过程.
解:∵D,B,E三点依次在线段AC上,
∴DE=+BE.
∵AD=BE,
∴DE=DB+=AB.
∵DE=4,
∴AB=4.
∵ ,
∴AC=2AB= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两名流感病人,如果每轮传播中平均一个病人传染的人数相同,为了使两轮传播后,流感病人总数不超过288人,则每轮传播中平均一个病人传染的人数不能超过人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a、b、c是同一平面内三条不重合的直线,则它们的交点可以有( )
A.1个或2个或3个
B.0个或1个或2个或3个
C.1个或2个
D.以上都不对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com