
����Ŀ����ͼ1����֪![]() �У�
��![]() ��
��![]() ��
��![]() ������ƽ��ֱ������ϵ��λ����ͼ��ʾ����
������ƽ��ֱ������ϵ��λ����ͼ��ʾ����![]() ��
��![]() ��ĸ������ϣ���
��ĸ������ϣ���![]() �ڵ�
�ڵ�![]() ���Ҳࣩ������
���Ҳࣩ������![]() �ڵڶ����ޣ���
�ڵڶ����ޣ���![]() ��
��![]() ���ڵ�ֱ�߷��ۣ���
���ڵ�ֱ�߷��ۣ���![]() ���ڵ�
���ڵ�![]() λ��
�
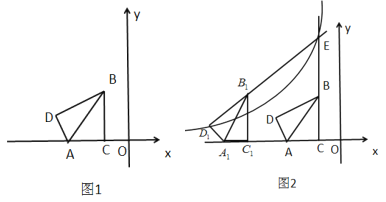
��1������![]() ����Ϊ
����Ϊ![]() ʱ�����
ʱ�����![]() �����ꣻ
�����ꣻ
��2������![]() �͵�
�͵�![]() ��ͬһ��������������ͼ���ϣ����
��ͬһ��������������ͼ���ϣ����![]() ���ꣻ
���ꣻ
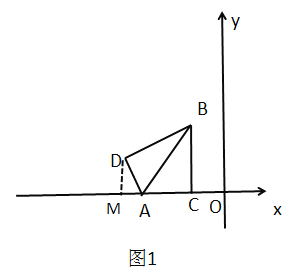
��3����ͼ2�����ı���![]() ����ƽ�ƣ�ƽ�ƺ���ı��μ����ı���
����ƽ�ƣ�ƽ�ƺ���ı��μ����ı���![]() ������
������![]() �ķ���������
�ķ���������![]() ��ͼ����
��ͼ����![]() ���ӳ��߽��ڵ�
���ӳ��߽��ڵ�![]() ������ƽ�ƹ����У��Ƿ����������
������ƽ�ƹ����У��Ƿ����������![]() ��ʹ���Ե�
��ʹ���Ե�![]() Ϊ�������������ֱ���������ҵ�
Ϊ�������������ֱ���������ҵ�![]() ��ͬһ��ֱ���ϣ������ڣ����
��ͬһ��ֱ���ϣ������ڣ����![]() ��ֵ���������ڣ���˵������
��ֵ���������ڣ���˵������
���𰸡���1��![]() ����2��
����2��![]() ����3�����ڣ�
����3�����ڣ�![]() ��
��![]()
��������
��1������![]() ��
��![]() ���ڵ�
���ڵ�![]() ���������Ǻ���ֵ�ɵó�
���������Ǻ���ֵ�ɵó�![]() ���ٸ��ݷ��۵����ʿɵó�
���ٸ��ݷ��۵����ʿɵó�![]() ��
��![]() ���ٽ�
���ٽ�![]() ���ó�
���ó�![]() ��
��![]() ������ϵ�C�����꼴�ɵó��𰸣�
������ϵ�C�����꼴�ɵó��𰸣�
��2�����![]() ����Ϊ
����Ϊ![]() ��
��![]() �������
�������![]() ��������
��������![]() �����ã�1���ó��Ľ����Ϊ��֪�������ɵó���D������Ϊ
�����ã�1���ó��Ľ����Ϊ��֪�������ɵó���D������Ϊ![]() ���ٽ�Ϸ�����������⼴�ɣ�
���ٽ�Ϸ�����������⼴�ɣ�
��3�����ȴ���������kֵ����![]() ��
��![]() ����������۷������ɣ�
����������۷������ɣ�
�⣺��1����ͼ������![]() ��
��![]() ���ڵ�
���ڵ�![]()
��![]() ��
��
��![]()
��![]()
�������֪![]() ��
��![]() .
.
��![]() .
.
��![]()
��![]() ��
��![]() ��
��
��![]() ��
��![]() .
.
�ߵ�![]() ����Ϊ
����Ϊ![]() ��
��
��![]() .
.
���![]() ��������
��������![]()
��2�����![]() ����Ϊ
����Ϊ![]() ��
��![]() �������
�������![]() ��������
��������![]() ��
��
�ɣ�1����֪����![]() ��������
��������![]()
�ߵ�![]() �͵�
�͵�![]() ��ͬһ��������������ͼ���ϣ�
��ͬһ��������������ͼ���ϣ�
��![]() .���
.���![]() .
.
���![]() ����Ϊ
����Ϊ![]()
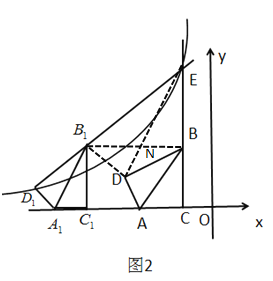
��3������������![]() ��ʹ���Ե�
��ʹ���Ե�![]() ��
��![]() ��
��![]() Ϊ�������������ֱ��������
Ϊ�������������ֱ��������
�⣺�ٵ�![]() ʱ.
ʱ.
��ͼ��ʾ������![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() .
.
��![]() ��
��![]() ��
��![]() .
.
��![]() ��
��![]()
��![]()
��![]()
�֡�![]() ��
��
��![]() ��
��![]() .
.
��![]() ��
��![]() ��
��
��![]() .
.
��![]() ��
��![]()
��![]() ��
��![]() ������
������![]() ��
��
��![]() ��
��![]() ��ͬһ����������ͼ���ϣ�
��ͬһ����������ͼ���ϣ�
��![]() .��ã�
.��ã�![]() .
.
��![]()
��![]()
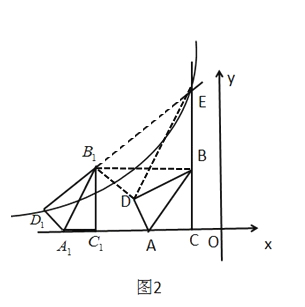
�ڵ�![]() ʱ.��ͼ��ʾ������
ʱ.��ͼ��ʾ������![]() ��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() .
.
��![]() ��
�У�
��![]() ��
��![]() ��
��
��![]() .
.
��![]() ��
�У�
��![]() ��
��
��![]() .
.
��![]()
��![]() ��
��![]() ������
������![]()
��![]() ��
��![]() ��ͬһ����������ͼ���ϣ�
��ͬһ����������ͼ���ϣ�
��![]() .
.
��ã�![]() ��
��
��![]()
��![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���������![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() ��õ�������
��õ�������![]() �����˷�ʽ���Ƶ�
�����˷�ʽ���Ƶ�![]() ������ת2019�εõ�������
������ת2019�εõ�������![]() �������
�������![]() ������Ϊ��1��0������ô��
������Ϊ��1��0������ô��![]() ������Ϊ________��
������Ϊ________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���֪��A��2![]() ��0����C��0����1������PΪ�߶�OA��һ���㣬��CP+
��0����C��0����1������PΪ�߶�OA��һ���㣬��CP+![]() AP����СֵΪ_____��
AP����СֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������ࡱ��ʶ���������ģ�����һ��ɷ�Ϊ���ɻ���������������к��������������������м�����һ������������������������
��1��ֱ��д�������õ�����ǡ���ǡ������������ĸ��ʣ�
��2���������õ�����������ͬ��ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������Ҫ�ڹ涨ʱ���ڰ���1200�ֻ���ԭ�ϣ�����![]() ��
��![]() ���ֻ����˿ɹ�ѡ����֪
���ֻ����˿ɹ�ѡ����֪![]() �ͻ����˱�
�ͻ����˱�![]() �ͻ�����ÿСʱ�����30���ͣ�
�ͻ�����ÿСʱ�����30���ͣ�![]() �����˰���900�����õ�ʱ����
�����˰���900�����õ�ʱ����![]() �ͻ����˰���600�����õ�ʱ����ȣ�
�ͻ����˰���600�����õ�ʱ����ȣ�
(1)�����ֻ�����ÿСʱ�ֱ���˶��ٶֻ���ԭ�ϣ�
(2)�ù���ԭ�ƻ�ͬʱʹ�������ֻ����˰��ˣ�����һ��ʱ���![]() �ͻ������������µİ����������뿪�������뱣֤��������ԭ����11Сʱ��ȫ��������ϣ���
�ͻ������������µİ����������뿪�������뱣֤��������ԭ����11Сʱ��ȫ��������ϣ���![]() �ͻ��������ٹ�������Сʱ�����ܱ�֤��������ԭ���ڹ涨��ʱ������ɣ�
�ͻ��������ٹ�������Сʱ�����ܱ�֤��������ԭ���ڹ涨��ʱ������ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
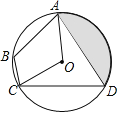
����Ŀ����ͼ����֪��O�İ뾶Ϊ2���ı���ABCD�ǡ�O���ڽ��ı��Σ���ABC����AOC����AD��CD����ͼ����Ӱ���ֵ��������______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������AOBC������ƽ��ֱ������ϵxOy�У���OA��y����������ϣ���OB��x����������ϣ������ߵĶ���ΪF���Գ��ύAC�ڵ�E���������߾�����A��0��2������C����D��3��0������AOB��ƽ������OE���������߶Գ�������ڵ�H������HF��
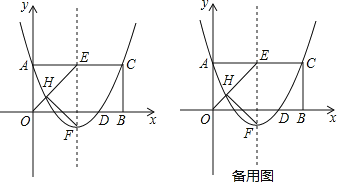
��1����������ߵĽ���ʽ��
��2����x�����ж���M���߶�BC���ж���N�����ı���EAMN���ܳ�����Сֵ��
��3�������������Ƿ���ڵ�P��ʹ���ı���EHFPΪƽ���ı��Σ�������ڣ������P�����ꣻ��������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y��ax2+bx+c��a��0��ͼ����ͼ��ʾ�����н��ۣ���abc��0����2a+b��0����a��b+c��0���ܵ�x��1ʱ��a+b��ax2+bx����4ac��b2��������ȷ���У���������
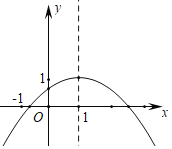
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
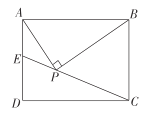
����Ŀ����ͼ���ھ���ABCD�У�![]() ���ھ�������һ��P��ͬʱ����
���ھ�������һ��P��ͬʱ����![]()
![]() ���ӳ�CP��AD�ڵ�E����
���ӳ�CP��AD�ڵ�E����![]() ______.
______.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com