
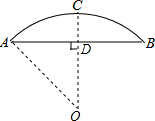
 如图所示,已知AB=16m,半径OA=10m,高度CD为4m.
如图所示,已知AB=16m,半径OA=10m,高度CD为4m.  各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:解答题
| 北京 | 天津西 | 济南 | 上海 | ||
| T13 | 到站时间 | … | 16:11 | 20:11 | 8:04 |
| 发车时间 | 14:40 | 16:16 | 20:23 | … | |
| T14 | 到站时间 | 9:03 | 7:23 | 3:14 | … |
| 发车时间 | … | 7:28 | 3:26 | 15:45 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | 0.8 | 2 | 3.2 | 4 | 5 | 8 |
| d(x) | 6a-3b+1 | 2a-b | 10a-5b | 4a-2b | 1-2a+b | 6a-3b |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知△ABC中,∠BAC=60°,BE、CD分别平分∠ABC、∠ACB,P为BE、CD的交点,连结AP,若AP=1,则AD+AE=$\sqrt{3}$.
如图,已知△ABC中,∠BAC=60°,BE、CD分别平分∠ABC、∠ACB,P为BE、CD的交点,连结AP,若AP=1,则AD+AE=$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,矩形ABCD中,AB=20,BC=10,点P为AB边上一动点,DP交AC于点Q.
如图,矩形ABCD中,AB=20,BC=10,点P为AB边上一动点,DP交AC于点Q.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com