

分析 (1)先找出相等条件,利用三角形全等的判定定理得出三角形全等,从而对应边相等得出结论.
(2)根据边角关系得出四边形ACDF为菱形,菱形的对角线互相垂直,证出结论.
解答 (1)证明:∵△ABC和△DEF是两块可以完全重合的三角板,
∴AB=DE,BC=EF,
又∵BF=BC-CF,EC=EF-CF,
∴BF=EC,
在△ABF和△DEC中,AB=DE,BF=EC,∠ABC=∠DEF,
∴△ABF≌△DEC(SAS),
∴AF=DC,
证毕.
(2)直线n与AD垂直,
证明:连接AD,如图,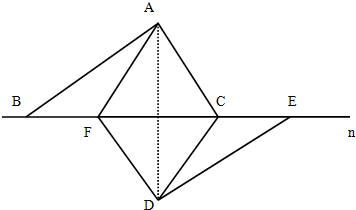
∵△ABC和△DEF是两块可以完全重合的三角板,且∠BAC=∠EDF=90°,∠ABC=∠DEF=30°,
∴∠ACB=∠DFE=60°,AC=DF,
∴AC∥DF,四边形ACDF为平行四边形,
在△DEF中,∠DFE=60°,∠DEF=30°,∠EDF=90°,且点C为线段EF的中点,
∴DC=CF=CE,
在△CDF中,DC=CF,∠DFE=60°,
∴△DCF为等边三角形,DF=DC,
又∵四边形ACDF为平行四边形,
∴四边形ACDF为菱形,
∴AD⊥CF,即AD⊥n,
证毕,
故直线n与AD垂直成立.
点评 本题考查了三角形的判定定理和菱形对角线互相垂直的性质,解题的关键是找对相等的边角.


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:解答题
 如图,两条互相平行的河岸,在河岸一边测得AB为20米,在另一边测得CD为70米,用测角器测得∠ACD=30°,测得∠BDC=45°,求两条河岸之间的距离.($\sqrt{2}≈1.4,\sqrt{3}$≈1.7,结果保留整数)
如图,两条互相平行的河岸,在河岸一边测得AB为20米,在另一边测得CD为70米,用测角器测得∠ACD=30°,测得∠BDC=45°,求两条河岸之间的距离.($\sqrt{2}≈1.4,\sqrt{3}$≈1.7,结果保留整数)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在三角形ABC中,∠C=90°,AB,AC,BC分别为5cm,3cm,4cm.
如图,在三角形ABC中,∠C=90°,AB,AC,BC分别为5cm,3cm,4cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com