
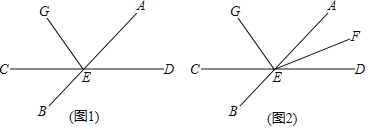
【题目】如图,直线AB与CD相交于点E,射线EG在∠AEC内(如图1).
(1)若∠BEC的补角是它的余角的3倍,则∠BEC= °;
(2)在(1)的条件下,若∠CEG比∠AEG小25度,求∠AEG的大小;
(3)若射线EF平分∠AED,∠FEG=m°(m>90°)(如图2),则∠AEG﹣∠CEG= °(用m的代表式表示).
【答案】(1)45°;(2)∠AEG=80°;(3)2m﹣180
【解析】
(1)设∠BEC=x°,根据题意,可列方程:180﹣x=3(90﹣x),解出∠BEC;
(2)由∠CEG=∠AEG﹣25°,得∠AEG=180°﹣∠BEC﹣∠CEG=180°﹣45°﹣(∠AEG﹣25°),解出∠AEG;
(3)计算出∠AEG和∠CEG,然后相减,即可得到结果.
解:(1)设∠BEC=x°,
根据题意,可列方程:180﹣x=3(90﹣x),
解得x=45°,
故∠BEC=45°,
故答案为:45°;
(2)∵∠CEG=∠AEG﹣25°,
∴∠AEG=180°﹣∠BEC﹣∠CEG
=180°﹣45°﹣(∠AEG﹣25°)=160°﹣∠AEG,
∴∠AEG=80°;
(3)∵EF平分∠AED,
∴∠AEF=∠DEF,
设∠AEF=∠DEF=α,∠AEG=∠FEG﹣∠AEF=m﹣α,
∠CEG=180°﹣∠GEF﹣DEF=180﹣m﹣α,
∴∠AEG﹣∠CEG=m﹣α﹣(180﹣m﹣α)=2m﹣180.
故答案为:2m﹣180.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,同时将点A(﹣1,0)、B(3,0)向上平移2个单位长度再向右平移1个单位长度,分别得到A、B的对应点C、D.连接AC,BD

(1)求点C、D的坐标,并描出A、B、C、D点,求四边形ABDC面积;
(2)在坐标轴上是否存在点P,连接PA、PC使S△PAC=S四边形ABCD?若存在,求点P坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古代阿拉伯数学家泰比特·伊本·奎拉对勾股定理进行了推广研究:如图(图1中![]() 为锐角,图2中
为锐角,图2中![]() 为直角,图3中
为直角,图3中![]() 为钝角).
为钝角).

在△ABC的边BC上取![]() ,
, ![]() 两点,使
两点,使![]() ,则
,则![]() ∽
∽![]() ∽
∽![]() ,
, ![]() ,
, ![]() ,进而可得
,进而可得![]()
![]() ;(用
;(用![]() 表示)
表示)
若AB=4,AC=3,BC=6,则![]()
![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,将点A翻折到对角线BD上的点M处,折痕BE交AD于点E.将点C翻折到对角线BD上的点N处,折痕DF交BC于点F.

(1)求证:四边形BFDE为平行四边形;
(2)若四边形BFDE为菱形,且AB=2,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“作一个30°角”的尺规作图过程.

请回答:该尺规作图的依据是______________________________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,现有一个均匀的转盘被平均分成6等份,分别标有数字2、3、4、5、6、7这六个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字.

求:(1)转动转盘,转出的数字大于3的概率是多少?
(2)现有两张分别写有3和4的卡片,随机转动转盘,转盘停止后记下转出的数字,与两张卡片上的数字分别作为三条线段的长度.
①这三条线段能构成三角形的概率是 .
②这三条线段能构成等腰三角形的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,则小巷的宽度为( )

A.2.2米B.2.3米C.2.4米D.2.5米
查看答案和解析>>
科目:初中数学 来源: 题型:
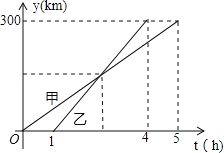
【题目】甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.则下列结论:①A,B两城相距300千米;②乙车比甲车晚出发1小时,却早到1小时; ③乙车出发后2小时追上甲车; ④当甲、乙两车相距50千米时,t=![]() 或
或![]() .其中正确的结论有_____.
.其中正确的结论有_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com