
【题目】如图,已知抛物线y=ax2+bx+4与x轴交于A(![]() ,0)、B两点,与y轴交于C点,其对称轴为直线x=1.
,0)、B两点,与y轴交于C点,其对称轴为直线x=1.
(1)直接写出抛物线的解析式 :
(2)把线段AC沿x轴向右平移,设平移后A、C的对应点分别为A′、C′,当C′落在抛物线上时,求A′、C′的坐标;
(3)除(2)中的点A′、C′外,在x轴和抛物线上是否还分别存在点E、F,使得以A、C、E、F为顶点的四边形为平行四边形,若存在,求出E、F的坐标;若不存在,请说明理由.

【答案】(1)![]() ;(2)(0,0),(2,4);(3)存在点E、F,使得以A、C、E、F为顶点的四边形为平行四边形,点E、F的坐标为:
;(2)(0,0),(2,4);(3)存在点E、F,使得以A、C、E、F为顶点的四边形为平行四边形,点E、F的坐标为:![]() 或
或![]() .
.
【解析】
试题(1)先求得B点的坐标,然后根据待定系数法交点抛物线的解析式:
∵A(![]() ,0),对称轴为直线x=1,∴B(4,0).
,0),对称轴为直线x=1,∴B(4,0).
把A(![]() ,0),B(4,0)代入抛物线的表达式得:
,0),B(4,0)代入抛物线的表达式得:
![]() ,解得:
,解得: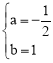 .
.
∴抛物线的解析式为:![]() .
.
(2)根据平移性质及抛物线的对称性,求出A′、C′的坐标.
(3)分AC为平行四边形的边和对角线两种情况讨论即可.
试题解析:解:(1)![]() .
.
(2)∵抛物线的解析式:![]() ,
,
∴当x=0时,y=4. ∴点C(0,4).
∵抛物线的对称轴为x=1,∴点C关于x=1的对称点C′的坐标为(2,4).
∴点C向右平移了2个单位长度.
∴则点A向右平移后的点A′的坐标为(0,0).
∴点A′,C′的坐标分别分(0,0),(2,4).
(3)存在.
设F(x,![]() ).
).
若以A、C、E、F为顶点的四边形为平行四边形,则:
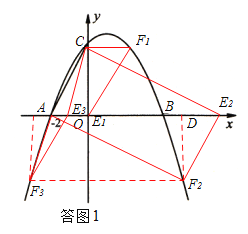
①AC为平行四边形的边,如答图1,
ⅰ)若CFEA为平行四边形,
则CF1∥AE1且CF1=AE1,
此时,E1,F1分别与点A′、C′重合,与题意不符,舍去.
ⅱ)若CEFA为平行四边形,则AC∥FE且AC=FE,
过点F2作F2D⊥x轴于点D,则易证Rt△AOC≌Rt△E2DF2,
∴DE=2,DF2=4.
∴![]() ,解得:
,解得:![]() .
.
∴![]() .
.
∴![]() .
.
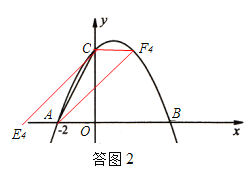
②若AC为平行四边形的对角线,如答图2.
则CF4∥E4A且CF4=E4A,
∴F4(2,4),E4(![]() ,0).
,0).
此时, F4与点C′重合,与题意不符,舍去.
综上所述,存在点E、F,使得以A、C、E、F为顶点的四边形为平行四边形,点E、F的坐标为:![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】图①是一个三角形,分别连接这个三角形三边的中点得到图②,再分别连接图②中间的小三角形三边的中点,得到图③.

(1)图②有__________个三角形;图③有________个三角形;
(2)按上面的方法继续下去,第10个图有_________个三角形,第![]() 个图形中有_______个三角形.(用含
个图形中有_______个三角形.(用含![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
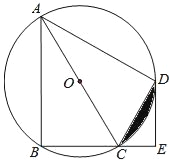
【题目】如图,四边形ABCD是⊙O的内接四边形,![]() ,AC为直径,DE⊥BC,垂足为E.
,AC为直径,DE⊥BC,垂足为E.
(1)求证:CD平分∠ACE;
(2)若AC=9,CE=3,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,且与正比例函数
,且与正比例函数![]() 的图象交于点
的图象交于点![]() .
.
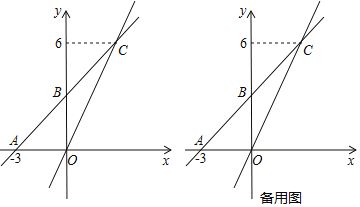
(1)求一次函数![]() 的解析式;
的解析式;
(2)点![]() 在
在![]() 轴上,当
轴上,当![]() 最小时,求出点
最小时,求出点![]() 的坐标;
的坐标;
(3)若点![]() 是直线
是直线![]() 上一点,点
上一点,点![]() 是平面内一点,以
是平面内一点,以![]() 、
、![]() 、
、![]() 、
、![]() 四点为顶点的四边形是矩形,请直接写出点
四点为顶点的四边形是矩形,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列两个等式:![]() ,
,![]() ,给出定义如下:我们称使等式
,给出定义如下:我们称使等式![]() 成立的一对有理数对“
成立的一对有理数对“![]() ,
,![]() ”为“共生有理数对”,记为
”为“共生有理数对”,记为![]() .
.
(1)通过计算判断数对“-4,2”,“7,![]() ”是不是“共生有理数对”;
”是不是“共生有理数对”;
(2)若![]() 是“共生有理数对”,则“
是“共生有理数对”,则“![]() ,
,![]() ”______(填“是”或“不是”)共生有理数对”,并说明理由.
”______(填“是”或“不是”)共生有理数对”,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小红玩抛硬币游戏,连续抛两次.小明说:“如果两次都是正面,那么你赢;如果两次是一正一反,则我赢.”小红赢的概率是__________,据此判断该游戏__________(填“公平”或“不公平”).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠A=∠D=90°,E、F在线段BC上,DE与AF交于点O,且AB=CD,BE=CF.
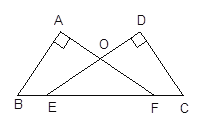
求证:(1)Rt△ABF≌Rt△DCE;(2)OE=OF .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校组织植树活动,已知在甲处植树的有220人,在乙处植树的有96人.
(1)若要使甲处植树的人数是乙处植树人数的3倍,应从乙处调多少人去甲处?
(2)为了尽快完成植树任务,现调m人去两处支援,其中![]() ,若要使甲处植树的人数仍然是乙处植树人数的3倍,则应调往甲,乙两处各多少人?
,若要使甲处植树的人数仍然是乙处植树人数的3倍,则应调往甲,乙两处各多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线![]() (
(![]() )与直线
)与直线![]() 相交于点P(2,m),与x轴交于点A.
相交于点P(2,m),与x轴交于点A.
(1)求m的值;
(2)过点P作PB⊥x轴于B,如果△PAB的面积为6,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com