
| A. | 3x=2y | B. | $\frac{x+y}{y}$=$\frac{5}{3}$ | C. | $\frac{x+1}{y+1}$=$\frac{3}{4}$ | D. | $\frac{x+2}{y+3}$=$\frac{x}{y}$ |
分析 根据比例的基本性质,合比性质,根据等式的性质,可得答案.
解答 解:A、由比例的性质,得3x=2y,故A正确;
B、由合比性质,得$\frac{x+y}{y}$=$\frac{5}{3}$,故B正确;
C、分子分母都加同一个数,分式的值发生变化,故C错误;
D、由比例的性质,得3x=2y,由等式的性质,得3x+xy=2y+xy,$\frac{x+2}{y}$=$\frac{x}{y}$,故D正确;
故选:C.
点评 本题考查了比例的性质,利用了比例的性质:外项的积等于内项的积,合比性质:$\frac{a}{b}$=$\frac{c}{d}$⇒$\frac{a+b}{b}$=$\frac{c+d}{d}$,等式的性质:等式的两边都加(或减)同一个数(或整式),结果不变,等式的两边都乘以(或除以)同一个不为零的数,结果不变.


科目:初中数学 来源: 题型:填空题
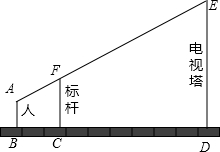 如图,某测量工作人员与标杆顶端F、电视塔顶端在同一直线上,已知此人眼睛距地面1.6米,标杆为3.2米,且BC=1米,CD=5米,则电视塔的高ED=11.2.
如图,某测量工作人员与标杆顶端F、电视塔顶端在同一直线上,已知此人眼睛距地面1.6米,标杆为3.2米,且BC=1米,CD=5米,则电视塔的高ED=11.2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 有两个相等的实数根 | B. | 可能有实数根,也可能没有 | ||
| C. | 有两个不相等的实数根 | D. | 没有实数根 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com