
【题目】角平分线上的点到角两边的距离相等.这一性质在解决图形面积问题时有何妙用呢?阅读材料:已知,如图(1),在面积为S的△ABC中,BC=a,AC=b,AB=c,三条角平分线的交点O到三边的距离为r.连接OA、OB、OC,△ABC被划分为三个小三角形.
∵S=S△OBC+S△OAC+S△OAB= ![]() BCr+
BCr+ ![]() ACr+
ACr+ ![]() ABr=
ABr= ![]() (a+b+c)r,∴r=
(a+b+c)r,∴r= ![]()

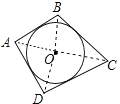
(1)类比推理:若面积为S的四边形ABCD的四条角平分线交于O点,如图(2),各边长分别为AB=a,BC=b,CD=c,AD=d,求点O到四边的距离r;
(2)理解应用:如图(3),在四边形ABCD中,AB∥DC,AB=21,CD=11,AD=BC=13,对角线BD=20,点O1与O2分别为△ABD与△BCD的三条角平分线的交点,设它们到各自三角形三边的距离为r1和r2 , 求 ![]() 的值.
的值.
【答案】
(1)解:如图,连接OA、OB、OC、OD,
∵S=S△AOB+S△BOC+S△COD+S△AOD= ![]() ar+
ar+ ![]() br+
br+ ![]() cr+
cr+ ![]() dr=
dr= ![]() (a+b+c)r,
(a+b+c)r,
∴r= ![]()
(2)解:∵AB∥CD,
∴S△ABD:S△BCD=AB:CD=21:11;
∵r1= ![]() =
= ![]() ,
,
r2= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() :
: ![]() =
= ![]() ×
× ![]() =
= ![]() =
= ![]()
【解析】(1)已知已给出示例,我们仿照例子,连接OA,OB,OC,OD,则四边形被分为四个小三角形,且每个三角形都以内切圆半径为高,以四边形各边作底,这与题目情形类似.仿照证明过程,r易得;(2)(1)中已告诉我们内切圆半径的求法,如是我们再相比即得结果.但求内切圆半径需首先知道三角形各边边长,根据等腰梯形性质,过点D作AB垂线,进一步易得BD的长,则r1、r2、 ![]() 易得.
易得.
【考点精析】解答此题的关键在于理解平行线的性质的相关知识,掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补,以及对角平分线的性质定理的理解,了解定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:
【题目】一种商品进价为每件100元,按进价增加20%出售,后因库存积压降价,按售价的九折出售,每件还能盈利( )
A. 8元B. 15元C. 12.5元D. 108元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若|m|=2,|n|=3,且在数轴上表示m的点与表示n的点分居原点的两侧,则下列哪个值可能是m+n的结果( )
A. 5B. -5C. -3D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知两点A(-4,0)、B(1,0),且以AB为直径的圆交![]() 轴的正半轴于点C(0,2),过点C作圆的切线交x轴于点D.
轴的正半轴于点C(0,2),过点C作圆的切线交x轴于点D.

(1)求过A, B,C三点的抛物线解析式;
(2)求点D的坐标;
(3)设平行于x轴的直线交抛物线于E,F两点,问是否存在以线段EF为直径的圆,恰好与x轴相切?若存在,求出该圆的半径,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】钓鱼岛是我国固有领土,位于我国东海,总面积约6340000平方米,数据6340000用科学记数法表示为( )
A.634×104
B.6.34×106
C.63.4×105
D.6.34×107
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A. 若线段AC=BC,则点C是线段AB的中点
B. 任何有理数的绝对值都不是负数
C. 角的大小与角两边的长度有关,边越长角越大
D. 两点之间,直线最短
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com