
����Ŀ������ʦ��1����������ɸ��������һ�������Ŀڴ��в����ȣ���ѧ�������������飬ÿ������һ���Żأ����±��ǻ�����е�һ��ͳ�����ݣ�
����Ĵ���n | 100 | 150 | 200 | 500 | 800 | 1000 |
��������Ĵ���m | 23 | 31 | 60 | 130 | 203 | 251 |
���������Ƶ�� | 0.23 | 0.21 | 0.30 | _____ | _____ | _____ |
��1����ȫ�ϱ��е��й����ݣ������ϱ����ݹ��ƴӴ�������һ������ĸ�����______�������������С�������λ��
��2��������а���ĸ���Ϊ________��
��3���ڣ�2���������£���Сǿͬѧ�зŻص��������������û���״ͼ���б��ķ�����������ζ���������ĸ��ʣ�
���𰸡����������ݣ�0.26��0.25��0.25 ��1��0.25����2��3����3��![]() ��
��
��������
(1)ֱ������Ƶ��������=Ƶ�������;
(2)������а�����x��,���ñ��������ݹ�����õ������Ƶ���г�����x�ķ�ʽ����,
��1��251��1000=0.251;
�ߴ����ظ������¼�������Ƶ�����ȶ���0.25����0.25,
����ƴӴ�������һ�����Ǻ���ĸ�����0.25;
��2������а���Ϊx��,
![]() =0.25,
=0.25,
x=3��
�𣺹��ƴ�����3������
��3�������⻭��״ͼ��:
����״ͼ��֪,���п��ܳ��ֵĽ������16��,��Щ������ֵĿ��������,�������ζ������������9�������
����P(�����������)=![]() ��
��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���![]() ��ͼ���뷴��������
��ͼ���뷴��������![]() ��ͼ���ཻ��A��2��1����B���㣮
��ͼ���ཻ��A��2��1����B���㣮

��1�����������������һ�κ����ı���ʽ��
��2����ֱ��д��B������꣬��ָ��ʹ����������ֵ����һ�κ���ֵ��x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧϰ���������֮��С��ͬѧ�������öԳơ���ת�ȷ������Լ���ȷ������������ķ�����
��1����������㽫����ͼ����ͼ����ͼ���ĵȱ������ηֱ���2����3����4��ȫ�������Σ�
��2����ͼ�����ȱߡ�ABC�߳�AB��4����OΪ�������ģ���M��N�ֱ�Ϊ��AB��BC�ϵĶ��㣨����˵��غϣ����ҡ�MON��120�㣬���ı���BMON�����Ϊs�������ܳ���Ϊl����![]() ��Сֵ��
��Сֵ��
��3����ͼ�����ȱߡ�ABC�ı߳�AB��4����PΪ��CA�ӳ�����һ�㣬��QΪ��AB�ӳ�����һ�㣬��DΪBC���е㣬�ҡ�PDQ��120�㣬��PA��x�����ú�x�Ĵ���ʽ��ʾ��BDQ�����S��BDQ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
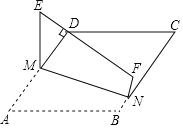
����Ŀ����ͼ��������ABCD�У�tanA��![]() ��M��N�ֱ��ڱ�AD��BC�ϣ����ı���AMNB��MN���ۣ�ʹAB�Ķ�Ӧ�߶�EF��������D����EF��ADʱ��
��M��N�ֱ��ڱ�AD��BC�ϣ����ı���AMNB��MN���ۣ�ʹAB�Ķ�Ӧ�߶�EF��������D����EF��ADʱ��![]() ��ֵΪ��������
��ֵΪ��������
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����20cm����12cm��ͼ������ͼ��������һ�������IJ������ᡢ�������Ŀ��ȱ�Ϊ3��2�����������Ŀ���Ϊxcm��ͼ��������������ռ���Ϊycm2��
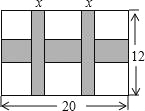
��1����y��x֮��ĺ�����ϵʽ��
��2����ͼ��������������ռ�����ͼ�������![]() ����ᡢ�������Ŀ��ȣ�
����ᡢ�������Ŀ��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ������⣺ѧϰ�˶��θ�ʽ����ᷢ��һЩ���и��ŵ�ʽ�ӿ���д����һ��ʽ�ӵ�ƽ������3+2![]() ����1+
����1+![]() ��2���������������µ�̽����
��2���������������µ�̽����
��a+b![]() ����m+n
����m+n![]() ��2������a��b��m��n������������������a+b
��2������a��b��m��n������������������a+b![]() ��m2+2n2+2mn
��m2+2n2+2mn![]() ����a��m2+2n2��b��2mn�������͵ó��˰�����a+b
����a��m2+2n2��b��2mn�������͵ó��˰�����a+b![]() ��ʽ�ӻ�Ϊƽ��ʽ�ķ������������������̽��������������⣺
��ʽ�ӻ�Ϊƽ��ʽ�ķ������������������̽��������������⣺
��1����a��b��m��n��Ϊ������ʱ����a+b![]() ����m+n
����m+n![]() ��2���ú�m��n��ʽ�ӷֱ��ʾa��b����a���� ����b���� ����
��2���ú�m��n��ʽ�ӷֱ��ʾa��b����a���� ����b���� ����
��2����a��4![]() ����m��n
����m��n![]() ��2��a��m��n��Ϊ����������a��ֵ��
��2��a��m��n��Ϊ����������a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
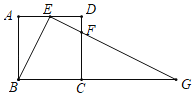
����Ŀ����ͼ����������ABCD�У�EΪ��AD���е㣬��F�ڱ�CD�ϣ��ҡ�BEF��90�����ӳ�EF��BC���ӳ����ڵ�G.
(1)��֤����ABE�ס�EGB.
(2)��AB��4����CG�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������ABC�ڽ��ڡ�O��CA��CB������A��AE��BC������O�ڵ�E������C����O�����߽�AE���ӳ����ڵ�D����֪AB��6��BE��3![]() ��
��
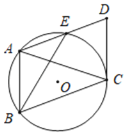
��1����֤���ı���ABCDΪƽ���ı��Σ�
��2���ӳ�AO��DC���ӳ����ڵ�F����AF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���κ���y=ax2+2x+c��ͼ����C��0��3������x��ֱ��ڵ�A����B��3��0������P��ֱ��BC�Ϸ�����������һ���㣮
��1������κ���y=ax2+2x+c�ı���ʽ��
��2������PO��PC��������POC��y�ᷭ�ۣ��õ��ı���POP��C�����ı���POP��CΪ���Σ��������ʱ��P�����ꣻ
��3������P�˶���ʲôλ��ʱ���ı���ACPB�������������ʱP���������ı���ACPB����������
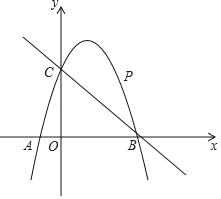
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com