
【题目】学习了正多边形之后,小马同学发现利用对称、旋转等方法可以计算等分正多边形面积的方案.
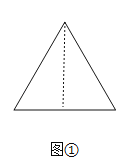
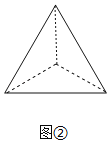
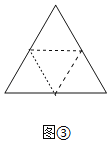
(1)请聪明的你将下面图①、图②、图③的等边三角形分别割成2个、3个、4个全等三角形;
(2)如图④,等边△ABC边长AB=4,点O为它的外心,点M、N分别为边AB、BC上的动点(不与端点重合),且∠MON=120°,若四边形BMON的面积为s,它的周长记为l,求![]() 最小值;
最小值;
(3)如图⑤,等边△ABC的边长AB=4,点P为边CA延长线上一点,点Q为边AB延长线上一点,点D为BC边中点,且∠PDQ=120°,若PA=x,请用含x的代数式表示△BDQ的面积S△BDQ.

【答案】(1)详见解析;(2)2+2![]() ;(3)S△BDQ
;(3)S△BDQ![]() x+
x+![]() .
.
【解析】
(1)根据要求利用全等三角形的判定和性质画出图形即可.
(2)如图④中,作OE⊥AB于E,OF⊥BC于F,连接OB.证明△OEM≌△OFN(ASA),推出EM=FN,ON=OM,S△EOM=S△NOF,推出S四边形BMON=S四边形BEOF=定值,证明Rt△OBE≌Rt△OBF(HL),推出BM+BN=BE+EM+BF﹣FN=2BE=定值,推出欲求![]() 最小值,只要求出l的最小值,因为l=BM+BN+ON+OM=定值+ON+OM所以欲求
最小值,只要求出l的最小值,因为l=BM+BN+ON+OM=定值+ON+OM所以欲求![]() 最小值,只要求出ON+OM的最小值,因为OM=ON,根据垂线段最短可知,当OM与OE重合时,OM定值最小,由此即可解决问题.
最小值,只要求出ON+OM的最小值,因为OM=ON,根据垂线段最短可知,当OM与OE重合时,OM定值最小,由此即可解决问题.
(3)如图⑤中,连接AD,作DE⊥AB于E,DF⊥AC于F.证明△PDF≌△QDE(ASA),即可解决问题.
解:(1)如图1,作一边上的中线可分割成2个全等三角形,
如图2,连接外心和各顶点的线段可分割成3个全等三角形,
如图3,连接各边的中点可分割成4个全等三角形,
(2)如图④中,作OE⊥AB于E,OF⊥BC于F,连接OB.
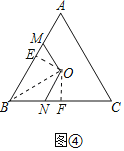
∵△ABC是等边三角形,O是外心,
∴OB平分∠ABC,∠ABC=60°∵OE⊥AB,OF⊥BC,
∴OE=OF,
∵∠OEB=∠OFB=90°,
∴∠EOF+∠EBF=180°,
∴∠EOF=∠NOM=120°,
∴∠EOM=∠FON,
∴△OEM≌△OFN(ASA),
∴EM=FN,ON=OM,S△EOM=S△NOF,
∴S四边形BMON=S四边形BEOF=定值,
∵OB=OB,OE=OF,∠OEB=∠OFB=90°,
∴Rt△OBE≌Rt△OBF(HL),
∴BE=BF,
∴BM+BN=BE+EM+BF﹣FN=2BE=定值,
∴欲求![]() 最小值,只要求出l的最小值,
最小值,只要求出l的最小值,
∵l=BM+BN+ON+OM=定值+ON+OM,
欲求![]() 最小值,只要求出ON+OM的最小值,
最小值,只要求出ON+OM的最小值,
∵OM=ON,根据垂线段最短可知,当OM与OE重合时,OM定值最小,
此时![]() 定值最小,s=
定值最小,s=![]() ×2×
×2×![]() =
=![]() ,l=2+2+
,l=2+2+![]() +
+![]() =4+
=4+![]() ,
,
∴![]() 的最小值=
的最小值=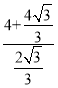 =2+2
=2+2![]() .
.
(3)如图⑤中,连接AD,作DE⊥AB于E,DF⊥AC于F.
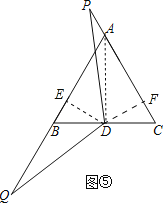
∵△ABC是等边三角形,BD=DC,
∴AD平分∠BAC,
∵DE⊥AB,DF⊥AC,
∴DE=DF,
∵∠DEA=∠DEQ=∠AFD=90°,
∴∠EAF+∠EDF=180°,
∵∠EAF=60°,
∴∠EDF=∠PDQ=120°,
∴∠PDF=∠QDE,
∴△PDF≌△QDE(ASA),
∴PF=EQ,
在Rt△DCF中,∵DC=2,∠C=60°,∠DFC=90°,
∴CF=![]() CD=1,DF=
CD=1,DF=![]() ,
,
同法可得:BE=1,DE=DF=![]() ,
,
∵AF=AC﹣CF=4﹣1=3,PA=x,
∴PF=EQ=3+x,
∴BQ=EQ﹣BE=2+x,
∴S△BDQ=![]() BQDE=
BQDE=![]() (2+x)×
(2+x)×![]() =
=![]() x+
x+![]() .
.


科目:初中数学 来源: 题型:
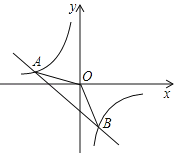
【题目】如图,一次函数y=kx+b与反比例函数y=![]() .(其中mk≠0)图象交于A(﹣4,2),B(2,n)两点.
.(其中mk≠0)图象交于A(﹣4,2),B(2,n)两点.
(1)求一次函数和反比例函数的表达式;
(2)求△ABO的面积;
(3)请直接写出当一次函数值大于反比例函数值时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
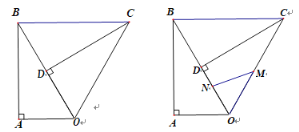
【题目】已知Rt△OAB,OAB90,ABO30,斜边OB4,将Rt△OAB绕点O顺时针旋转60,得到△COD,如图1,连接BC.
(1)求BC的长度;
(2)如图2,点M,N同时从点O出发,在△OCB边上运动,M沿OCB路径匀速运动,N沿OBC路径匀速运动,当两点相遇时运动停止,已知点M的运动速度为1.5个单位/秒,点N的运动速度为1个单位/秒,设运动时间为x秒,△OMN的面积为y,求y关于x的函数解析式,并直接写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某小区楼房附近有一个斜坡,坡角为30°,小王发现楼房在水平地面与斜坡处形成的投影中,在斜坡上的影子长CD=6m,坡脚到楼房的距离CB=8m.在D点处观察点A的仰角为60°.求楼房AB的高度(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)某调查小组采用简单随机抽样方法,对某市部分中小学生一天中阳光体育运动时间进行了抽样调查,并把所得数据整理后绘制成如下的统计图:
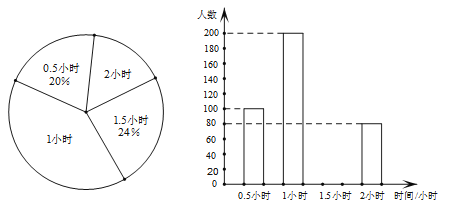
(1)该调查小组抽取的样本容量是多少?
(2)求样本学生中阳光体育运动时间为1.5小时的人数,并补全占频数分布直方图;
(3)请估计该市中小学生一天中阳光体育运动的平均时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
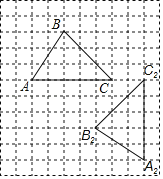
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,△ABC为格点三角形(顶点在网格线的交点).
(1)将△ABC向上平移2个单位得到△A1B1C1,请画出△A1B1C1;
(2)将△ABC绕着某点O逆时针方向旋转90°后,得到△A2B2C2,请画出旋转中心O,并直接写出在此旋转过程中,线段AB扫过的区域的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由我国完全自主设计、自主建造的首艘国产航母于2018年5月成功完成第一次海上试验任务.如图,航母由西向东航行,到达![]() 处时,测得小岛
处时,测得小岛![]() 位于它的北偏东
位于它的北偏东![]() 方向,且与航母相距80海里,再航行一段时间后到达B处,测得小岛
方向,且与航母相距80海里,再航行一段时间后到达B处,测得小岛![]() 位于它的北偏东
位于它的北偏东![]() 方向.如果航母继续航行至小岛
方向.如果航母继续航行至小岛![]() 的正南方向的
的正南方向的![]() 处,求还需航行的距离
处,求还需航行的距离![]() 的长.
的长.
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李老师将1个黑球和若干个白球放入一个不透明的口袋中并搅匀,让学生进行摸球试验,每次摸出一个球(放回),下表是活动进行中的一组统计数据.
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到黑球的次数m | 23 | 31 | 60 | 130 | 203 | 251 |
摸到黑球的频率 | 0.23 | 0.21 | 0.30 | _____ | _____ | _____ |
(1)补全上表中的有关数据,根据上表数据估计从袋中摸出一个黑球的概率是______.(结果都保留小数点后两位)
(2)估算袋中白球的个数为________.
(3)在(2)的条件下,若小强同学有放回地连续两次摸球,用画树状图或列表的方法计算出两次都摸出白球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线C1:y=ax2﹣![]() x+2(a>0)与x轴交于A、B(点A在点B左侧),与y轴交于点C.
x+2(a>0)与x轴交于A、B(点A在点B左侧),与y轴交于点C.
(1)如图1,若A(2,0),连AC、BC.
①直接写出C1的解析式及△ABC的面积;
②将△AOC绕某一点逆时针旋转90°至△A′O′C′(其中A、O、C的对应点分别为A′、O′、C′).若旋转后的△A′O′C′恰有一边的两个端点落在抛物线C1的图象上,求点A′的坐标;
(2)如图2,平移抛物线C1使平移后的新抛物线C2顶点在原点,P(![]() ,0)是x轴正半轴上一点,过P作直线交C2的图象于A、B,过A的直线y=x+b交C2于点C,过P作x轴的垂线交BC于点M,设点M的纵坐标为n,试判断an是否为定值?若是,求这个定值,若不是,说明理由.
,0)是x轴正半轴上一点,过P作直线交C2的图象于A、B,过A的直线y=x+b交C2于点C,过P作x轴的垂线交BC于点M,设点M的纵坐标为n,试判断an是否为定值?若是,求这个定值,若不是,说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com