
【题目】如图,一次函数y=kx+b与反比例函数y=![]() .(其中mk≠0)图象交于A(﹣4,2),B(2,n)两点.
.(其中mk≠0)图象交于A(﹣4,2),B(2,n)两点.
(1)求一次函数和反比例函数的表达式;
(2)求△ABO的面积;
(3)请直接写出当一次函数值大于反比例函数值时x的取值范围.
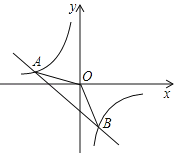
【答案】(1)y=﹣x﹣2,y=﹣![]() ;(2)6;(3)x<﹣4或0<x<2.
;(2)6;(3)x<﹣4或0<x<2.
【解析】
(1)把A点坐标分别代入一次函数和反比例函数的解析式中,即可解得k、b、m、n的值;
(2)求出一次函数y=kx+b与x轴的交点坐标,然后根据三角形的面积公式即可求出△ABO的面积;
(3)根据图象观察,当x<﹣4或0<x<2时,一次函数值大于反比例函数值.
解:(1)∵一次函数y=kx+b与反比例函数y=![]() (mk≠0)图象交于A(﹣4,2),B(2,n)两点.
(mk≠0)图象交于A(﹣4,2),B(2,n)两点.
根据反比例函数图象的对称性可知,n=﹣4,
∴![]() ,解得
,解得![]() ,
,
故一次函数的解析式为y=﹣x﹣2,
又知A点在反比例函数的图象上,故m=﹣8,
故反比例函数的解析式为y=﹣![]() ;
;
(2)如图,设一次函数的图像与y轴交于点C,
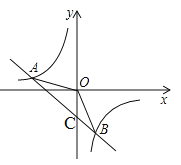
在y=﹣x﹣2中,令x=0,则y=﹣2,
∴OC=2,
∴S△AOB=![]()
![]() ×2×2+
×2×2+![]() ×2×4=6;
×2×4=6;
(3)根据两函数的图象可知:
当x<﹣4或0<x<2时,一次函数值大于反比例函数值.


科目:初中数学 来源: 题型:
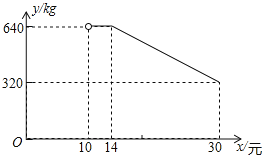
【题目】郧西县下营村是我市出名的“淘宝村”,该乡镇开始了多家网店,销售当地农产品,某网店在网上销售一种当地特产,其成本为每千克10元,在销售期间发现,每天销售量![]() 与销售单价
与销售单价![]() (元)满足如图所示的函数关系(其中
(元)满足如图所示的函数关系(其中![]() ).
).
(1)写出![]() 与
与![]() 之间的函数关系式及自变量的取值范围;
之间的函数关系式及自变量的取值范围;
(2)若要使每天销售该特产的利润要达到3100元,则销售单价![]() 应定为多少元?
应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,其关于
,其关于![]() 轴对称的抛物线为
轴对称的抛物线为![]() :
:![]() ,且
,且![]() 经过点
经过点![]() 和点
和点![]() .
.
(1)求抛物线![]() 的解析式;
的解析式;
(2)将抛物线![]() 沿
沿![]() 轴向右平移得到抛物线
轴向右平移得到抛物线![]() ,抛物线
,抛物线![]() 与
与![]() 轴的交点记为点
轴的交点记为点![]() 和点
和点![]() (
(![]() 在
在![]() 的右侧),与
的右侧),与![]() 轴交于点
轴交于点![]() ,如果满足
,如果满足![]() 与
与![]() 相似,请求出平移后抛物线
相似,请求出平移后抛物线![]() 的表达式.
的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区教育系统为了更好地宣传扫黑除恶专项斗争,印制了应知应会手册,该区教育局想了解教师对扫黑除恶专项斗争应知应会知识掌握程度,抽取了部分教师进行了测试,并将测试成绩绘制成下面两幅统计图,请根据统计图中提供的信息,回答下面问题:
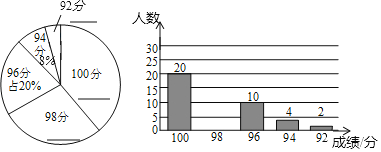
(1)计算样本中,成绩为98分的教师有 人,并补全两个统计图;
(2)样本中,测试成绩的众数是 ,中位数是 ;
(3)若该区共有教师6880名,根据此次成绩估计该区大约有多少名教师已全部掌握扫黑除恶专项斗争应知应会知识?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了疫情防控需要,某防护用品厂计划生产150000个口罩,但是在实际生产时,……,求实际每天生产口罩的个数,在这个题目中,若设实际每天生产口罩x个,可得方程![]() =10,则题目中用“……”表示的条件应是( )
=10,则题目中用“……”表示的条件应是( )
A.每天比原计划多生产500个,结果延期10天完成
B.每天比原计划少生产500个,结果提前10天完成
C.每天比原计划少生产500个,结果延期10天完成
D.每天比原计划多生产500个,结果提前10天完成
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:![]() ,AB=10米,AE=15米.(i=1:
,AB=10米,AE=15米.(i=1:![]() 是指坡面的铅直高度BH与水平宽度AH的比)
是指坡面的铅直高度BH与水平宽度AH的比)

(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米.参考数据:![]() 1.414,
1.414,![]() 1.732)
1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
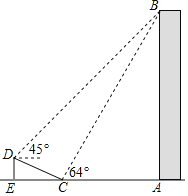
【题目】如图,在大楼AB的正前方有一斜坡CD,CD=13米,坡比DE:EC=1: ![]() ,高为DE,在斜坡下的点C处测得楼顶B的仰角为64°,在斜坡上的点D处测得楼顶B的仰角为45°,其中A、C、E在同一直线上.
,高为DE,在斜坡下的点C处测得楼顶B的仰角为64°,在斜坡上的点D处测得楼顶B的仰角为45°,其中A、C、E在同一直线上.
(1)求斜坡CD的高度DE;
(2)求大楼AB的高度;(参考数据:sin64°≈0.9,tan64°≈2).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为开展“阳光体育”活动,计划拿出不超过3000元的资金购买一批篮球,羽毛球拍和乒乓球拍,已知篮球,羽毛球拍和乒乓球拍的单价比为8:3:2,且其单价和为130元,
(1)请问篮球,羽毛球拍和乒乓球拍的单价分别是多少元?
(2)若要求购买篮球,羽毛球拍和乒乓球拍的总数量是80个(副),羽毛球拍的数量是乒乓球拍数量的4倍,且购买乒乓球拍的数量不超过15副请问有几种购买方案?哪种方案,才能使运费最少?最少运费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售一种商品,童威经市场调查发现:该商品的周销售量![]() (件)是售价
(件)是售价![]() (元/件)的一次函数,其售价、周销售量、周销售利润
(元/件)的一次函数,其售价、周销售量、周销售利润![]() (元)的三组对应值如下表:
(元)的三组对应值如下表:
售价 | 50 | 60 | 80 |
周销售量 | 100 | 80 | 40 |
周销售利润 | 1000 | 1600 | 1600 |
注:周销售利润=周销售量×(售价-进价)
(1)①求![]() 关于
关于![]() 的函数解析式(不要求写出自变量的取值范围)
的函数解析式(不要求写出自变量的取值范围)
②该商品进价是_________元/件;当售价是________元/件时,周销售利润最大,最大利润是__________元
(2)由于某种原因,该商品进价提高了![]() 元/件
元/件![]() ,物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求
,物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求![]() 的值
的值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com