
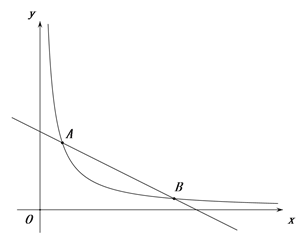
【题目】如图,一次函数y=-![]() x+b与反比例函数y=
x+b与反比例函数y=![]() (x>0)的图象交于点A(2,6)和B(m,1)
(x>0)的图象交于点A(2,6)和B(m,1)
(1)填空:一次函数的解析式为 ,反比例函数的解析式为 ;
(2)点E为y轴上一个动点,若S△AEB=5,求点E的坐标.
【答案】(1)y=﹣![]() x+7,y=
x+7,y=![]() (2)(0,6)或(0,8)
(2)(0,6)或(0,8)
【解析】分析:(1)把点A的坐标分别代入一次函数y与反比例函数,可得b,k的值,从而得到结论.
(2)把B(m,1)代入反比例函数,得到m的值,从而得到B的坐标.设直线AB与y轴的交点为P,点E的坐标为(0,a),连接AE,BE,则点P的坐标为(0,7),得到PE=|a﹣7|.由S△AEB=S△BEP﹣S△AEP=5, 可求得a的值,从而得到点E的坐标.
详解:(1)∵一次函数y=-![]() x+b与反比例函数y=
x+b与反比例函数y=![]() (x>0)的图象交于点A(2,6),∴6=
(x>0)的图象交于点A(2,6),∴6=![]() ,k=2×6=12,解得:b=7,k=12.∴一次函数的解析式为
,k=2×6=12,解得:b=7,k=12.∴一次函数的解析式为![]() ,反比例函数的解析式为
,反比例函数的解析式为![]() .
.
(2)∵B(m,1)在反比例函数![]() 上,∴1=
上,∴1=![]() ,解得:m=12,∴B(12,1).
,解得:m=12,∴B(12,1).
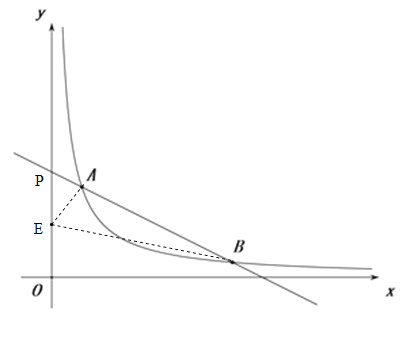
如图,直线AB与y轴的交点为P,设点E的坐标为(0,a),连接AE,BE,
则点P的坐标为(0,7).
∴PE=|a﹣7|.
∵S△AEB=S△BEP﹣S△AEP=5,
∴![]() ×|a﹣7|×(12﹣2)=5.
×|a﹣7|×(12﹣2)=5.
∴|a﹣7|=1.
∴a1=6,a2=8.
∴点E的坐标为(0,6)或(0,8).


科目:初中数学 来源: 题型:
【题目】已知:如图,O为正方形ABCD的中心,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连接DF,交BE的延长线于点G,连接OG.
(1)求证:△BCE≌△DCF;
(2)OG与BF有什么数量关系?证明你的结论;
(3)若GE·GB=4-2![]() ,求正方形ABCD的面积.
,求正方形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列方程中哪些是一元二次方程?将一元二次方程写成一般式的形式,并指出它的二次项系数、一次项系数和常数项
(1)![]() ;
;
(2)![]() ;
;
(3)![]() ;
;
(4)![]() ;
;
(5)![]() ;
;
(6)![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】公元9世纪,阿拉伯数学家阿尔花拉子米在他的名著《代数学》中用图解一元二次方程,他把一元二次方程![]() 写成
写成![]() 的形式,并将方程左边的
的形式,并将方程左边的![]() 看作是由一个正方形(边长为
看作是由一个正方形(边长为![]() )和两个同样的矩形(一边长为
)和两个同样的矩形(一边长为![]() ,另一边长为
,另一边长为![]() )构成的矩尺形,它的面积为
)构成的矩尺形,它的面积为![]() ,如图所示。于是只要在这个图形上添加一个小正方形,即可得到一个完整的大正方形,这个大正方形的面积可以表小为:
,如图所示。于是只要在这个图形上添加一个小正方形,即可得到一个完整的大正方形,这个大正方形的面积可以表小为:![]() ____
____![]() _______ ,整理,得
_______ ,整理,得![]() ,因为
,因为![]() 表示边长,所以
表示边长,所以![]() ___________.
___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】光明玩具公司要生产若干件高级玩具,现有甲、乙两个加工厂都想加工这批玩具,已知甲厂单独加工这批玩具比乙厂单独加工这批玩具多用20天,甲厂每天可加工16件玩具,乙厂每天可加工24件玩具,玩具公司每天需付给甲厂800元加工费,每天需付给乙厂1200元加工费.
(1)这个玩具公司要生产多少件高级玩具?
(2)在加工过程中,玩具公司需派一名技术员每天到加工厂进行指导,并为该技术员提供每天20元的午餐补助,玩具公司制订玩具加工方案如下:可由一个厂单独加工完成,也可由两厂合作完成.请你帮助玩具公司选择一种既省钱又省时的加工方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1:在等边△ABC中,点D,E分别在边AB,AC上,AD=AE,连结BE,CD,点M、N、P分别是BE、CD、BC的中点.
(1)观察猜想
图1中△PMN的形状是 ;
(2)探究证明
把△ADE绕点A逆时针方向旋转到图2的位置,△PMN的形状是否发生改变?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+bx+c交y轴于点A(0,4),交x轴于点B(4,0),点P是抛物线上一动点,过点P作x轴的垂线PQ,过点A作AQ⊥PQ于点Q,连接AP.
(1)填空:抛物线的解析式为 ,点C的坐标 ;
(2)点P在抛物线上运动,若△AQP∽△AOC,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是“明清影视城”的一扇圆弧形门,小红到影视城游玩,他了解到这扇门的相关数据:这扇圆弧形门所在的圆与水平地面是相切的,AB=CD=0.25米,BD=1.5米,且AB.CD与水平地面都是垂直的.根据以上数据,请你帮小红计算出这扇圆弧形门的最高点离地面的距离是( )
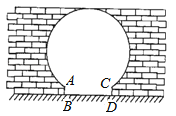
A.2米 B.2.5米 C.2.4米 D.2.1米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明,下面是小聪利用图1证明勾股定理的过程:

将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°,求证:a2+b2=c2
证明:连接DB,过点D作BC边上的高DF,则DF=EC=b﹣a.
∵S四边形ADCB=S△ACD+S△ABC=![]() b2+
b2+![]() ab.
ab.
又∵S四边形ADCB=S△ADB+S△DCB=![]() c2+
c2+![]() a(b﹣a)
a(b﹣a)
∴![]() b2+
b2+![]() ab=
ab=![]() c2+
c2+![]() a(b﹣a)
a(b﹣a)
∴a2+b2=c2
请参照上述证法,利用图2完成下面的证明.
将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°.求证:a2+b2=c2
证明:连结______,过点B作________,则____________.
∵S五边形ACBED=S△ACB+S△ABE+S△ADE=____________.
又∵S五边形ACBED=______________=![]() ab+
ab+![]() c2+
c2+![]() a(b﹣a),
a(b﹣a),
∴___________________=![]() ab+
ab+![]() c2+
c2+![]() a(b﹣a),
a(b﹣a),
∴a2+b2=c2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com