
1)问题发现
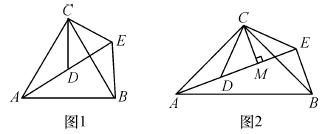
如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.
填空:①∠AEB的度数为 ;
②线段AD、BE之间的数量关系是 .
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.请判断∠AEB的度数及线段CM、AE、BE之间的数量关系,并说明理由.
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源:2014-2015学年重庆开县八年级上学期期末考试数学试卷(解析版) 题型:选择题
要使分式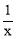 有意义,x的取值范围满足( )
有意义,x的取值范围满足( )
A.x=0 B.x≠0 C.x>0 D.x<0
查看答案和解析>>
科目:初中数学 来源: 题型:
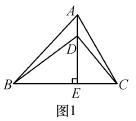
如图1,在△ABC中,AE⊥BC于E,AE=BE,D是AE上的一点,且DE=CE,连接BD、AC.
(1)试判断BD与AC的位置关系和数量关系,并说明理由.
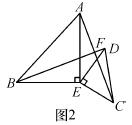
(2)如图2,若将△DCE绕点E旋转一定的角度后,试判断BD与AC的位置关系和数量关系是否发生变化,并说明理由.
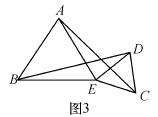
(3)如图3,若将(2)中的等腰直角三角形都换成等边三角形,其他条件不变,
①试猜想BD与AC的数量关系,并说明理由.
②你能求出BD与AC的夹角度数吗?如果能,请直接写出夹角度数;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省兴化顾庄等三校八年级上学期期末考试数学试卷(解析版) 题型:选择题
如果点P(m ,1-2m)在第一象限,那么m的取值范围是( )
A.0<m<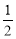 B.-
B.-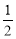 <m<0 C.m<0 D. m>
<m<0 C.m<0 D. m>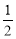
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,湖中的小岛上有一标志性建筑物,其底部为A,某人在岸边的B处测得A在B的北偏东30°的方向上,然后沿岸边直行4公里到达C处,测得A在C的北偏西45°的方向上(其中A、B、C在同一个平面上).求这个标志性建筑物的底部A到岸边BC的最短距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com