
【题目】计算
(1)![]()
(2)![]()
(3)![]()
(4)
【答案】(1)﹣![]() ;(2)6;(3)
;(2)6;(3)![]() ;(4)
;(4) .
.
【解析】
(1)根据二次根式的除法运算法则计算,再合并同类二次根式即可;
(2)根据二次根式的乘法运算法则计算,再合并同类二次根式即可;
(3)加减消元法求解即可:①+②×2,解出x的值,再代入原方程,求得y即可;
(4)利用换元法,设x+y=m,x﹣y=n,先解关于m和n的二元一次方程组,再解得x和y的值.
解:(1)![]()
=![]()
=![]()
=![]()
=﹣![]() ;
;
(2)![]()
=![]() ×
×![]() +
+![]() ×
×![]() ﹣6
﹣6![]()
=6![]() +6﹣6
+6﹣6![]()
=6;
(3) ,
,
①+②×2得:7x=21,
∴x=3
将x=3代入②得:2×3﹣y=8,
∴y=﹣2,
∴方程组的解为![]() .
.
(4)设x+y=m,x﹣y=n,原方程组可化为:
 ,
,
①﹣②×6得:﹣4n﹣n=4﹣6,
∴n=![]() ③,
③,
将③代入②得: ,
,
∴m=![]() ,
,
∴ ,
,
∴ .
.


科目:初中数学 来源: 题型:
【题目】操作探究:
数学研究课上,老师带领大家探究《折纸中的数学问题》时,出示如图1所示的长方形纸条ABCD,其中AD=BC=1,AB=CD=5.然后在纸条上任意画一条截线段MN,将纸片沿MN折叠,MB与DN交于点K,得到△MNK.如图2所示:

探究:
(1)若∠1=70°,∠MKN= °;
(2)改变折痕MN位置,△MNK始终是 三角形,请说明理由;
应用:
(3)爱动脑筋的小明在研究△MNK的面积时,发现KN边上的高始终是个不变的值.根据这一发现,他很快研究出△KMN的面积最小值为![]() ,此时∠1的大小可以为 °
,此时∠1的大小可以为 °
(4)小明继续动手操作,发现了△MNK面积的最大值.请你求出这个最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
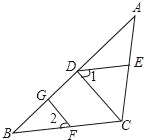
【题目】如图,已知FG⊥AB,CD⊥AB,垂足分别为G,D,∠1=∠2,
求证:∠CED+∠ACB=180°,
请你将小明的证明过程补充完整.
证明:∵FG⊥AB,CD⊥AB,垂足分别为G,D(已知)
∴∠FGB=∠CDB=90°( ).
∴GF∥CD( )
∵GF∥CD(已证)
∴∠2=∠BCD( )
又∵∠1=∠2(已知)
∴∠1=∠BCD( )
∴ ( )
∴∠CED+∠ACB=180°( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】生活与数学
(1)莹莹在日历上圈出三个数,呈大写的“一”字,这三个数的和是中间数的 倍,莹莹又在日历上圈出5个数,呈“十”字框形,它们的和是50,则中间的数是 :
(2)小丽同学也在某月的日历上圈出如图所示“七”字形,发现这八个数的和是125,那么这八个数中最大数为 :
(3)在第(2)题中这八个数之和 为101(填“能”或“不能”).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列小金鱼图案是用长度相同的小木棒按一定规律拼搭而成,第一条小金鱼图案需8根小木棒,第二条小金鱼图案需14根小木棒,…,按此规律,
(1)第n条小金鱼图案需要小木棒 根;
(2)如果有30000根小木棒,按照如图所示拼搭第1条,第2条……,直到第100条金鱼,请通过计算说明这些木棒是否够用.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(一)阅读
求x+6x+11的最小值.
解:x+6x+11
=x2+6x+9+2
=(x+3)2+2
由于(x+3)2的值必定为非负数,所以(x+3)2+2,即x2+6x+11的最小值为2.

(二)解决问题
(1)若m2+2mn+2n2-6n+9=0,求(![]() )-3的值;
)-3的值;
(2)对于多项式x2+y-2x+2y+5,当x,y取何值时有最小值,最小值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】儿童节期间,某公园游戏场举行一场活动.有一种游戏的规则是:在一个装有8个红球和若干白球(每个球除颜色外,其他都相同)的袋中,随机摸一个球,摸到一个红球就得到一个海宝玩具.已知参加这种游戏的儿童有40 000人,公园游戏场发放海宝玩具8 000个.
(1)求参加此次活动得到海宝玩具的频率?
(2)请你估计袋中白球的数量接近多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com