【题目】已知二次函数
.
（1）求出抛物线的顶点坐标、对称轴、最小值；
（2）求出抛物线与x轴、y轴交点坐标；
【答案】（1） 顶点坐标（－2，－4.5），对称轴：直线x＝－2；最小值－4.5;（2）抛物线与x轴的交点坐标为（－5，0），（1，0）．与y轴的交点坐标为（0，
）
【解析】
（1）首先把已知函数解析式配方，然后利用抛物线的顶点坐标、对称轴的公式即可求解；
（2）根据抛物线与x轴、y轴交点坐标特点和函数解析式即可求解．
解：（1）∵
∴顶点坐标（-2，-
），对称轴：直线x=-2；
因为二次项系数大于0，所以函数有最小值-；
（2）令y=0，则
x2+2x-
=0，
解得x=-5，x=1．
所以抛物线与x轴的交点坐标为（-5，0），（1，0）；
令x=0，则y=-．
所以抛物线与y轴的交点坐标为（0，-）．
每日10分钟口算心算速算天天练系列答案科目：初中数学 来源： 题型：
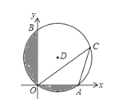
【题目】如图，在平面直角坐标系中，已知⊙D经过原点O，与x轴、y轴分别交于A、B两点，B点坐标为（0，
），OC与⊙D交于点C，∠OCA＝30°.求
（1）⊙D的半径；
（2）圆中阴影部分的面积（结果保留根号和π）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，将△ABC的高AD四等分，过每一个分点作底边的平行线，把三角形的面积分成四部分S1、S2、S3、S4，则S1：S2：S3：S4等于（ ）
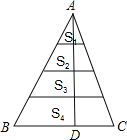
A.1：2：3：4B.2：3：4：5C.1：3：5：7D.3：5：7：9
查看答案和解析>>
科目：初中数学 来源： 题型：
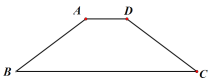
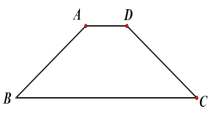
【题目】如图，在等腰梯形ABCD中，AD//BC,AD=2，AB=5，BC=10，点E是边BC上的一个动点（不与B,C重合），作∠AEF=∠AEB,使边EF交边CD于点F,(不与C，D重合），线段BE=______________时，△ABE与△CEF相似。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图有一座抛物线形拱桥，桥下面在正常水位是AB宽20m，水位上升3m就达到警戒线CD，这是水面宽度为10m。
（1）在如图的坐标系中求抛物线的解析式。
(2)若洪水到来时，水位以每小时0.2m的速度上升，从警戒线开始，再持续多少小时才能到拱桥顶？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某工厂用
天时间生产一款新型节能产品，每天生产的该产品被某网店以每件
元的价格全部订购，在生产过程中，由于技术的不断更新，该产品第
天的生产成本
（元/件）与（天）之间的关系如图所示，第天该产品的生产量
（件）与（天）满足关系式
第
天，该厂生产该产品的利润是 元；
设第天该厂生产该产品的利润为
元．
①求与之间的函数关系式，并指出第几天的利润最大，最大利润是多少？
②在生产该产品的过程中，当天利润不低于
元的共有多少天？
查看答案和解析>>
科目：初中数学 来源： 题型：
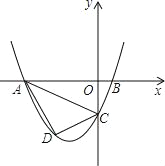
【题目】已知，抛物线y=ax2+3ax+c（a＞0）与y轴交于点C，与x轴交于A，B两点，点A在点B左侧．点B的坐标为（1，0），OC=3OB．
(1)直接写出C点的坐标；
(2)求抛物线的解析式；
(3)若点D是线段AC下方抛物线上的动点，求四边形ABCD面积的最大值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数的图象与x轴交于A（－2，0）、B（3，0）两点，且函数有最大值是2.
（1）求二次函数的图象的解析式；
（2）设此二次函数的顶点为P，求△ABP的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
