练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】Rt△ABC中，∠C＝90°，AC＝3，BC＝4，若以点C为圆心，r为半径，且⊙C与斜边AB有唯一公共点，求半径r的取值范围．

    【答案】3＜r≤4或r＝2.4．

    【解析】

    先根据勾股定理求得AB＝5，然后分两种情况：

    （1）圆与AB相切时，即r＝CD＝3×4÷5＝2.4；

    （2）点A在圆内部，点B在圆上或圆外时，此时AC＜r≤BC，即3＜r≤4．

    ∴3＜r≤4或r＝2.4．

    如图，∵BC＞AC，

    以C为圆心，r为半径所作的圆与斜边AB只有一个公共点．

    根据勾股定理求得AB＝5．

    分两种情况：

    （1）圆与AB相切时，即r＝CD＝3×4÷5＝2.4；

    （2）点A在圆内部，点B在圆上或圆外时，此时AC＜r≤BC，即3＜r≤4．

    ∴3＜r≤4或r＝2.4．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，AB、CB、CD分别与⊙O切于E，F，G，且AB∥CD．连接OB、OC，延长CO交⊙O于点M，过点M作MN∥OB交CD于N．

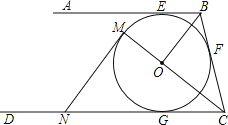
    （1）当OB＝6cm，OC＝8cm时，求⊙O的半径；

    （2）求证：MN＝NG．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，矩形ABCD中，AB=4，BC=6，以A、D为圆心，半径分别为2和1画圆，E、F分别是⊙A、⊙D上的一动点，P是BC上的一动点，则PE+PF的最小值是( )

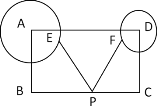
    A.5B.6C.7D.8

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,己知等边△ABC中,AB=8.以AB为直径的半⊙O与边AC相交于点D.过点D作DE⊥BC,垂足为E,过点E作EF⊥AB,垂足为F、连接DF.

    (1)求证:DE是⊙O的切线

    (2)求EF的长;

    (3)求sin∠EFD的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解方程：

    （1）4x2﹣8x+1＝0；

    （2）7x（5x+2）＝6（5x+2）；

    （3）3x2+5（2x+1）＝0；

    （4）x（x﹣1）＝2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】关于抛物线y＝x2－（a＋1）x＋a－2，下列说法错误的是（　　）

    A. 开口向上 B. 当a＝2时，经过坐标原点O

    C. a＞0时，对称轴在y轴左侧 D. 不论a为何值，都经过定点（1，－2）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

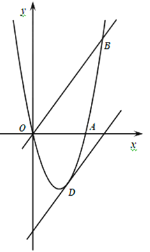
    【题目】如图：已知抛物线y＝ax2＋bx(a≠0)经过A（3，0），B（4，4）两点.

    （1）求抛物线解析式.

    （2）将直线OB向下平移m个单位后，得到的直线与抛物线只有一个公共点D，求m值及交点D的坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知实数a，b满足a﹣b＝1，a2﹣ab+1＞0，当2≤x≤3时，二次函数y＝a（x﹣1）2+1（a≠0）的最大值是3，求a的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列说法正确的是（　　）

    A.一颗质地均匀的骰子已连续抛投了2015次，其中抛掷出5点的次数最少，则第2016次一定抛掷出5点

    B.某种彩票中奖的概率是1%，因此买100张该种彩票一定会中奖

    C.天气预报说明天下雨的概率是，所以明天将有一半时间在下雨

    D.在同一年出生的367名学生中，至少有两人的生日是同一天

    查看答案和解析>>

    同步练习册答案