
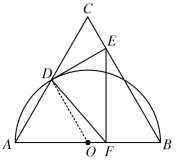
【题目】如图,己知等边△ABC中,AB=8.以AB为直径的半⊙O与边AC相交于点D.过点D作DE⊥BC,垂足为E,过点E作EF⊥AB,垂足为F、连接DF.

(1)求证:DE是⊙O的切线
(2)求EF的长;
(3)求sin∠EFD的值.
【答案】(1)见解析;(2)EF=3![]() ;(3)
;(3)![]()
【解析】
(1)先判断出△AOD是等边三角形,进而得出OD∥BC,推出DE⊥OD即可得出结论;
(2)先求出CD=4,在Rt△CDE中利用30°所对的直角边是斜边的一半求出CE,即可求出BE,然后在Rt△BEF中可求EF;
(3)先求出OG,DG,再求出BF,即可求出FG,利用勾股定理求出DF,即可得出结论.
(1)如图,连接OD,
∵OA=OD
∴∠A=∠ADO,
∵△ABC是等边三角形,
∴∠A=∠B=60°,
∴∠A=∠ADO=60°,
∴△AOD是等边三角形,
∴∠AOD=60°=∠B,
∴OD∥BC,
∵DE⊥BC,
∴DE⊥OD,
∵点D在⊙O上,
∴DE是⊙O的切线;
(2)由(1)知,OD∥BC,
∵OA=OB,
∴AD=CD,
∵AC=AB=8,
∴CD=4,
在Rt△CDE中,∠C=60°,
∴∠CDE=30°,
∴CE=![]() CD=2,
CD=2,
∴BE=BC-CE=6,
在Rt△BEF中,∠B=60°,
∴∠BEF=30°,
∴EF=BEcos∠BEF=6×cos30°=![]()
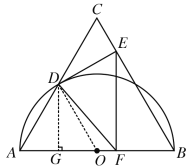
(3)如图,连接DF,OD,过点D作DG⊥AB于G,
∵EF⊥AB,
∴EF∥DG
∴∠EFD=∠GDF,
∵△AOD是等边三角形,
∴OG=![]() OA=2,
OA=2,
∴DG=OG·tan∠AOD=![]()
在Rt△BEF中,∠BEF=30°,BE=6,
∴BF=![]() BE=3
BE=3
∴OF=OB-BF=4-3=1
∴FG=OG+OF=![]()
在Rt△DGF中,根据勾股定理得,DF=![]()
∴sin∠EFD=sin∠GDF=![]()


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】如图,圆锥母线的长l等于底面半径r的4倍,
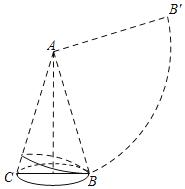
(1)求它的侧面展开图的圆心角.
(2)当圆锥的底面半径r=4cm时,求从B点出发沿圆锥侧面绕一圈回到B点的最短路径的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于60元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 50 | 60 | 70 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)求售价为多少元时每天获得利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
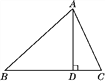
【题目】如图,在△ABC中,AD是BC边上的高,tanB=cos∠DAC.
(1)求证:AC=BD;
(2)若sin C=![]() ,BC=12,求△ABC的面积.
,BC=12,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某楼盘准备以每平方米15000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米12150元的均价开盘销售
![]() 求平均每次下调的百分率.
求平均每次下调的百分率.
![]() 某人准备以开盘价均价购买一套100平方米的住房,开发商给予以下两种优惠方案以供选择:
某人准备以开盘价均价购买一套100平方米的住房,开发商给予以下两种优惠方案以供选择:
![]() 打
打![]() 折销售;
折销售;![]() 不打折,一次性送装修费每平方米250元.
不打折,一次性送装修费每平方米250元.
试问哪种方案更优惠?比另外一种方案优惠多少元?![]() 不考虑其他因素
不考虑其他因素![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种爆竹点燃后,其上升高度h(米)和时间t(秒)符合关系式h=v0t+![]() gt2(0<t≤2),其中重力加速度g以10米/秒2计算.这种爆竹点燃后以v0=20米/秒的初速度上升.(上升过程中,重力加速度g为﹣10米/秒2;下降过程中,重力加速度g为10米/秒2)
gt2(0<t≤2),其中重力加速度g以10米/秒2计算.这种爆竹点燃后以v0=20米/秒的初速度上升.(上升过程中,重力加速度g为﹣10米/秒2;下降过程中,重力加速度g为10米/秒2)
(1)这种爆竹在地面上点燃后,经过多少时间离地15米?
(2)在爆竹点燃后的1.5秒至1.8秒这段时间内,判断爆竹是上升,或是下降,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,△ABC在直角坐标系内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2)(正方形网格中每个小正方形的边长均为一个单位长度).

①画出△ABC向下平移4个单位长度得到的△A1B1C1 , 点C1的坐标是________;
②以点B为位似中心,在网格内画出△A2B2C2 , 使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是________;
③若M(a,b)为线段AC上任一点,写出点M的对应点M2的坐标________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com