
【题目】如图,圆锥母线的长l等于底面半径r的4倍,
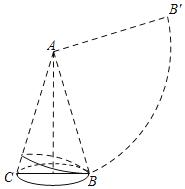
(1)求它的侧面展开图的圆心角.
(2)当圆锥的底面半径r=4cm时,求从B点出发沿圆锥侧面绕一圈回到B点的最短路径的长
【答案】(1)它的侧面展开图的圆心角为90°;(2)BB′=8![]() .
.
【解析】
(1)设它的侧面展开图的圆心角为n°,利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和弧长公式得到2πr=![]() ,然后求出n的值即可;
,然后求出n的值即可;
(2)连接BB′,如图,根据两点之间线段对短得到BB′为从B点出发沿圆锥侧面绕一圈回到B点的最短路径,然后利用△ABB′为等腰直角三角形得到BB′的长.
解:(1)设它的侧面展开图的圆心角为n°,
根据题意得2πr=![]() ,
,
而l=2r,
所以2πr=![]() ,解得n=90,
,解得n=90,
所以它的侧面展开图的圆心角为90°;
(2)连接BB′,如图,
此时BB′为从B点出发沿圆锥侧面绕一圈回到B点的最短路径,
∵r=4,
∴l=2r=8,
∵∠BAB′=90°,
∴△ABB′为等腰直角三角形,
∴BB′=![]() AB=8
AB=8![]() .
.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:
【题目】已知如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点BD是对角线,AG∥DB,交CB的延长线于G,连接GF,若AD⊥BD.下列结论:①DE∥BF;②四边形BEDF是菱形;③FG⊥AB;④S△BFG=![]() .其中正确的是( )
.其中正确的是( )

A. ①②③④ B. ①② C. ①③ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,与x轴的一个交点在(-3,0)和(-2,0)之间,其部分图象如图,则下列结论:①4ac-b2<0;②2a-b=0;③a+b+c<0;④点(x1,y1),(x2,y2)在抛物线上,若x1<x2,则y1<y2 .正确结论的个数是( )
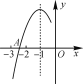
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某快餐店共有10名员工,所有员工工资的情况如下表:
人员 | 店长 | 厨师甲 | 厨师乙 | 会计 | 服务员甲 | 服务员乙 | 勤杂工 |
人数 | 1 | 1 | 1 | 1 | 1 | 3 | 2 |
工资额 | 20000 | 7000 | 4000 | 2500 | 2200 | 1800 | 1200 |
请解答下列问题:
(1)餐厅所有员工的平均工资是 ;所有员工工资的中位数是 .
(2)用平均数还是用中位数描述该餐厅员工工资的一般水平比较恰当?
(3)去掉店长和厨师甲的工资后,其他员工的平均工资是多少?它是否也能反映该快餐店员工工资的一般水平?
查看答案和解析>>
科目:初中数学 来源: 题型:
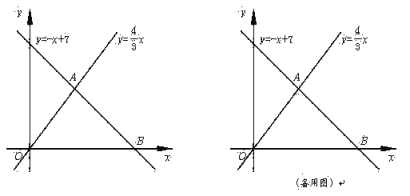
【题目】如图,已知一次函数y=-x+7与正比例函数y=![]() x的图像交于点A,且与x轴交于点B.
x的图像交于点A,且与x轴交于点B.
(1)求点A和点B的坐标;
(2)过点A作AC⊥y轴于点C,过点B作直线l∥y轴.动点P从点O出发,以每秒1个单位长的速度,沿O—C—A的路线向点A运动;同时直线l从点B出发,以相同速度向左平移,在平移过程中,直线l交x轴于点R,交线段BA或线段AO于点Q.当点P到达点A时,点P和直线l都停止运动.在运动过程中,设动点P运动的时间为t秒.
①当t为何值时,以A、P、R为顶点的三角形的面积为8?
②是否存在以A、P、Q为顶点的三角形是等腰三角形?若存在,求t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是一块绿化带,将阴影部分修建为花圃,已知AB=15,AC=9,BC=12,阴影部分是△ABC的内切圆,一只自由飞翔的小鸟将随机落在这块绿化带上,则小鸟落在花圃上的概率为______.
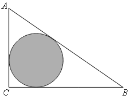
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB、CB、CD分别与⊙O切于E,F,G,且AB∥CD.连接OB、OC,延长CO交⊙O于点M,过点M作MN∥OB交CD于N.
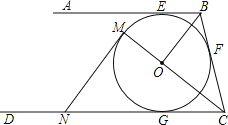
(1)当OB=6cm,OC=8cm时,求⊙O的半径;
(2)求证:MN=NG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某数学兴趣小组为测量教学楼CD的高,先在A处用高1.5米的测角仪测得教学楼顶端D的仰角∠DEG为30°,再向前走20米到达B处,又测得教学楼顶端D的仰角∠DFG为60°,A、B、C三点在同一水平线上,求教学楼CD的高(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,己知等边△ABC中,AB=8.以AB为直径的半⊙O与边AC相交于点D.过点D作DE⊥BC,垂足为E,过点E作EF⊥AB,垂足为F、连接DF.

(1)求证:DE是⊙O的切线
(2)求EF的长;
(3)求sin∠EFD的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com